Cauchy's Theorems.
Let
![$ C:[a,b] \longrightarrow \mathbb{C}$](/images/maths/complex-analysis/cauchy-th/img865.png) be a path of integration. It is smooth at a point
be a path of integration. It is smooth at a point
![$ t_0 \in [a,b]$](/images/maths/complex-analysis/cauchy-th/img866.png) if
if
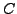 is derivable at
is derivable at
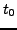 and if its first derivative is continuous at
and if its first derivative is continuous at
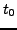
. The path is smooth if it is smooth at every point; it is smooth by parts if it
is not smooth at only a finite number of points.
Example 5.3.1
The arc
of the parabola whose equation is
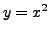
is smooth.
Figure 2: Paths.
![\begin{figure}\mbox{ \subfigure[smooth]{\epsfig{file=smootharc1.eps,height=3cm}}...
...mooth at one
point]{\epsfig{file=nonsmootharc1.eps,height=3cm}} }\end{figure}](/images/maths/complex-analysis/cauchy-th/img869.png) |
A loop is an integrating path whose origin and endpoints are
identical. If it is smooth and does not intersect itself at another point, we
will call it a Jordan curve. If we travel exactly once along the loop, we
will call it a simple loop. The integral of a function
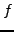 along a simple loop
along a simple loop
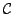 will be denoted as follows:
will be denoted as follows:
Note the little circle on the integration symbol.
A Jordan curve determines in the plane three disjoint regions: the curve
itself, the interior (= a bounded region) and the exterior (= an unbounded
region).
Note that the converse is not true: if
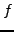 is not analytic on the interior of
is not analytic on the interior of
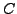 , the integral
, the integral
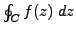 can either vanish or not. For example, compute the following integral:
can either vanish or not. For example, compute the following integral:
Using the parametrization
![$ z=\cos t + i \; \sin t, \; t\in [0,2 \pi ]$](/images/maths/complex-analysis/cauchy-th/img876.png) , we can show that
, we can show that
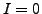 . The integral vanishes, despite the fact that the function fails to be analytic
at 0, which is an interior point of the unit circle (defined here by the
equation
. The integral vanishes, despite the fact that the function fails to be analytic
at 0, which is an interior point of the unit circle (defined here by the
equation
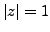 ).
).
Example 5.3.3
-
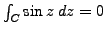 , for every Jordan curve
, for every Jordan curve
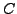 in the Cauchy-Argand plane.
in the Cauchy-Argand plane.
- Let
 and let
and let
 be the unit circle. As
be the unit circle. As
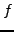 is analytic on the closed unit disk, we have:
is analytic on the closed unit disk, we have:
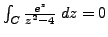 .
.
Corollary 5.3.4
Let
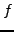 be a function defined and analytic on a connected domain
be a function defined and analytic on a connected domain
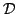 . Let
. Let
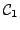 and
and
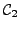 be two paths with the same origin
be two paths with the same origin
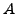 and the same endpoint
and the same endpoint
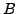 such that both path contain only interior points of
such that both path contain only interior points of
 (see Figure
3).
Then
(see Figure
3).
Then
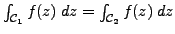 .
.
Figure 3: Two paths
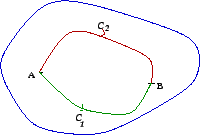 |
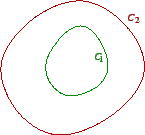
Figure 4: Loop within loop.
 |
|