Cauchy-Riemann Equations.
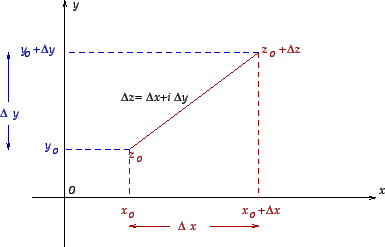
Recall the definition of the derivative of a function
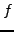 at a point
at a point
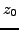 :
:
Denote:
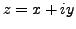 ,
,
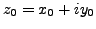 ,
,
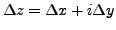 and
and
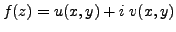 , where , where
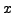 ,
,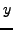 ,
,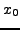 ,
,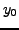 ,
,
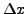 , ,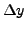 ,
,
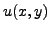 and
and
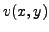 are real.
are real.
Figure 1: Cauchy-Riemann.
 |
Suppose that
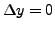 ; thus we have:
; thus we have:
Suppose that
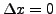 ; thus we have:
; thus we have:
Hence we have the so-called Cauchy-Riemann Equations:
which can be wriiten in the following form, with a notation frequently used in
Calculus:
Theorem 3.3.1
If
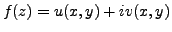 is derivable at
is derivable at
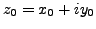 , then
, then
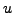 and
and
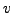 verify the Cauchy-Riemann Equations at
verify the Cauchy-Riemann Equations at
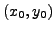 .
.
Example 3.3.2
Let
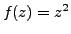
. As a polynomial function,
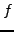
is derivable over the whole of
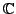
.
Let us check the Cauchy-Riemann equations. Denote
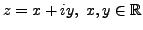 . Then we have:
. Then we have:
It follows that:
at every point in the plane, i.e. Cauchy-Riemann equations hold everywhere.
There is a kind of inverse theorem:
Theorem 3.3.4
If
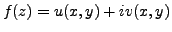 verifies the Cauchy-Riemann Formulas at
verifies the Cauchy-Riemann Formulas at
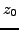 and if the partial derivatives of
and if the partial derivatives of
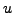 and
and
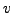 are continuous at
are continuous at
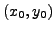 , the
, the
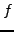 is derivable at
is derivable at
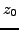 and
and
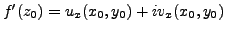 .
.
Example 3.3.6
Let
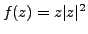
, for any
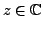
. We work as in the previous examples:
We compute the first partial derivatives:
We solve Cauchy-Riemann equations:
The subset of the plane where
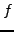 can be differentiable is the union of the two coordinate axes. As the first
partial derivatives of
can be differentiable is the union of the two coordinate axes. As the first
partial derivatives of
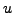 and
and
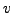 are continuous at every point in the plane,
are continuous at every point in the plane,
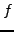 is differentiable at every point on one of the coordinate axes.
is differentiable at every point on one of the coordinate axes.
Cauchy-Riemann equations in polar form:
Instead of
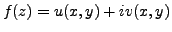 , write
, write
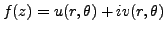 , where
, where
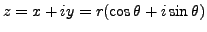 . .
|