Equations of degree 2.
We solve the equation
where
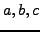 are complex numbers and
are complex numbers and
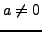 .
.
We have:
Define
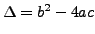 .
.
- If
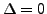 , then
, then
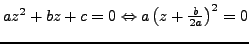 . The equation has a double solution, namely
. The equation has a double solution, namely
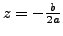 .
.
-
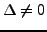 , then
, then
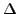 has two complex square roots; we denote them
has two complex square roots; we denote them
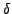 and
and
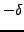 . Thus:
. Thus:
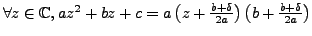 .
.
The equation has two distinct complex solutions, namely:
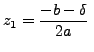 and
and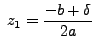 |
|
Example 1.6.1
Solve the equation
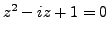
, where
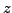
is a complex unknown.
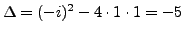 . Thus,
. Thus,
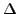 has two complex square roots, namely
has two complex square roots, namely
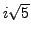 and
and
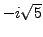 . The solutions
. The solutions
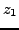 and
and
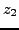 of the equation are given by:
of the equation are given by:
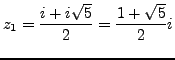 and
and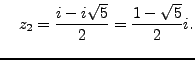 |
|
Example 1.6.2
Solve the equation
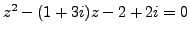
, where
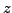
is a complex unknown.
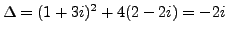 . The complex square roots of
. The complex square roots of
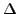 are
are
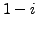 and
and
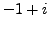 (You can compute them either by the algebraic method, described in
subsection 5.3,
or by the trigonometric method, described in subsection 5.1).
(You can compute them either by the algebraic method, described in
subsection 5.3,
or by the trigonometric method, described in subsection 5.1).
The solutions
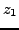 and
and
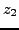 of the equation are given by:
of the equation are given by:
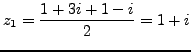 and
and
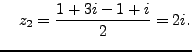 |
|