Derivation.
Definition 3.2.1
Let
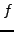
be a function defined on a domain
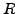
in
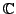
and let
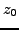
be an interior point of
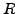
. The function
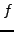
is derivable (or
differentiable) at
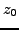
if there exists a complex number
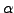
such that
We denote this by
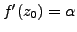
.
Remark 3.2.2
Another formulation of Def. 2.1
is as follows:
Example 3.2.3
Let
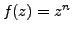
, where
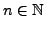
. Then, for every
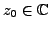
:
from what follows:
The function
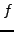
is differentiable at every point
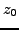
and
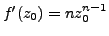
.
The algebra of derivable functions of a complex variable is (formally)
identical to the algebra of derivable functions of a real variable seen in
Calculus.
Example 3.2.5
If
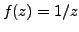
, then
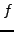
is differentiable at every point of
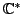
and
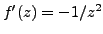
.
As easy consequences of Proposition 2.4,
we have Corollary 2.7
and Corollary 2.8 .
Corollary 3.2.7
A polynomial function is differentiable on the whole of
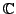 .
.
Corollary 3.2.8
A rational function is differentiable at every point of its domain
of definition
Example 3.2.9
The function
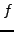
such that
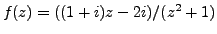
is differentiable on
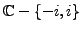
and we have:
Actually, we do not dispose of enough functions in order to display more
interseting examples. For that purpose, we shall wait until next chapter (i.e.
Chapter chapter analytic functions).
|