Geometric representation of complex numbers.
Let
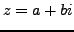 , with real
, with real
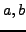 . To this complex number we associate the point
. To this complex number we associate the point
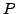 and the vector
and the vector
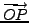 , both with coordinates
, both with coordinates
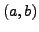
.
When used to represent complex numbers, the Euclidean plane is called the
Cauchy-Argand plane or Gauss
plane. Biographies of Augustin Cauchy (1789-1857) and Jean Argand
(1768-1822) can be found in The MacTutor History of Mathematics archive, at the
following URL:
$z+z'=(a+c)+(b+d)i$
A biography
Figure 1: Augustin Cauchy.
 |
Let
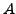 and
and
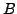 be two points with respective ``complex coordinate''
be two points with respective ``complex coordinate''
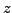 and
and
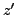 . Then
. Then
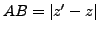 .
.
Figure 2: Distances and
circles.
![\begin{figure}\mbox{
\subfigure[]{\epsfig{file=vector.eps,height=3cm}}
\qquad \qquad
\subfigure[]{\epsfig{file=circle.eps,height=3cm}}
}\end{figure}](/images/maths/complex-analysis/geometric/img140.png) |
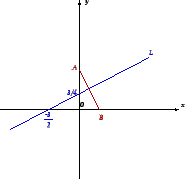
Example 1.2.1
(A perpendicular bisector) Represent in the plane the set of complex
numbers
such that
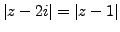
.
Geometrically, the given equation represents the set of all the points
 at the equal distances from the points
at the equal distances from the points
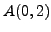 and
and
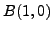 , i.e. the perpendicular bisector of the segment
, i.e. the perpendicular bisector of the segment
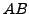 .
.
Let
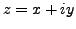 , where
, where
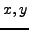 are real. We have:
are real. We have:
This is the equation of the perpendicular bisector of
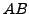 (see Figure 3).
(see Figure 3).
Figure 3: A perpendicular
bisector.
 |
Example 1.2.2
(Circles.) If
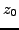
is the complex coordinate of a point
in the plane, then the circle whose center is in
and whose radius is equal to
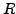
is defined by the equation
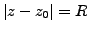
(see Figure 2(b)).
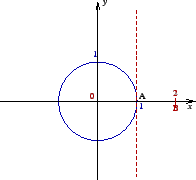
Example 1.2.3
(A solved exercise.) Find the geometric locus of all the points
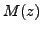
in the complex plane such that
On the one hand we have:
Thus, the required geometric locus is contained in the unit circle.
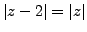 if, and only if, the point
if, and only if, the point
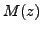 is on the perpendicular bisector of the segment whose endponts are the
origin and the point
is on the perpendicular bisector of the segment whose endponts are the
origin and the point
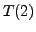 . Therefore the
. Therefore the
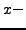 coordinate of
coordinate of
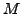 is equal to 1.
is equal to 1.
It follows that the required geometric locus is made of all the points on
the unit circle whose
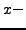 coordinate is equal to 1; it contains exactly one point, namely
coordinate is equal to 1; it contains exactly one point, namely
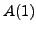 ; see Figure
44.
; see Figure
44.
Figure 4: Intersection of
the unit circle and a line.
 |
|