Integrals of the form
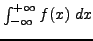 .
.
In calculus, we define an improper (real) integral with
two infinite limits
as follows:
We can compute such integrals using integrals of functions of a complex
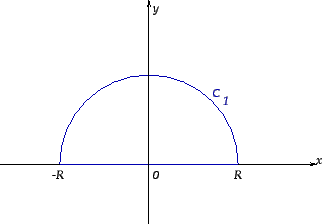
variable. Consider the loop
 consisting of the segment
consisting of the segment
![$ [-R,R]$](/images/maths/complex-analysis/integral/img1199.png) on the
on the
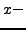 axis and the upper semicircle
axis and the upper semicircle
 defined by
defined by
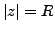 (with
(with
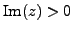 ),as in Figure
1, choosing
),as in Figure
1, choosing
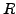 such that this loop encloses all the singular points of the complex function
such that this loop encloses all the singular points of the complex function
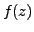 which are in the upper half-plane.
which are in the upper half-plane.
Figure 1: Upper semicircle.
 |
Then we compute the integral
We can show that
thus
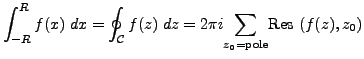 |
(9.1) |
Example 9.3.1
We compute the integral
Let
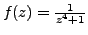 . This function has 4 poles in the complex plane,
. This function has 4 poles in the complex plane,
namely the solutions of
the equation
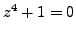 . These poles are:
. These poles are:
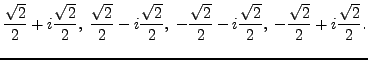 |
(9.2) |
Thus we have:
Let
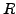 be a positive real number such that all of these poles with positive
imaginary part are inside the loop defined as above, namely the first and
the fourth of the numbers listed in
6; these are
be a positive real number such that all of these poles with positive
imaginary part are inside the loop defined as above, namely the first and
the fourth of the numbers listed in
6; these are
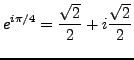 and
and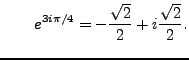 |
(9.3) |
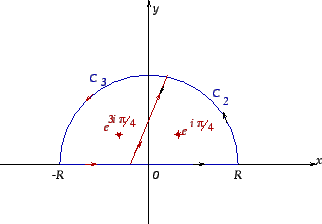
Now we compute the residues of
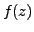 at each of these points; in what follows,
at each of these points; in what follows,
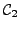 and
and
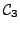 are simple loops obtained by ``cutting''
are simple loops obtained by ``cutting''
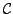 into two parts, such that
into two parts, such that
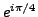 is an
interior point of is an
interior point of
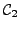 , but not of
, but not of
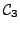 , and
, and
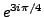 is an interior point of
is an interior point of
 , but not of
, but not of
 (cf Figure
2).
(cf Figure
2).
Figure 2: Two simple loops
in an upper semicircle.
 |
Thus, we have:
|