Looking for GATE Preparation Material? Join & Get here now!

** Gate 2013 Question Papers.. ** CEED 2013 Results.. ** Gate 2013 Question Papers With Solutions.. ** GATE 2013 CUT-OFFs.. ** GATE 2013 Results.. **

Laurent Series

Laurent Series.

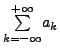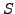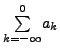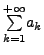The series $\underset{k=- \infty}{\overset{+ \infty}{\sum}} a_k$ is convergent and as as its sum if both $\underset{k=- \infty}{\overset{0}{\sum}} a_k$ and $\underset{k=1}{\overset{+ \infty}{\sum}} a_k$ are convergent and if its sum is equal to the sum of the sums of these series.

Theorem 8.2.1 Take $f(z)= \underset{k=- \infty}{\overset{+ \infty}{\sum}} a_k z^k$ .

The series is convergent in the domain $D=\{ z \in \mathbb{C}; \; r<\vert z\vert<R \}$ , where

$\displaystyle r=\underset{k \rightarrow + \infty}{\text{lim sup}} \vert a_{-k}\... ...rac {1}{\underset{k \rightarrow + \infty}{\text{lim sup}}} \vert a_k\vert^{1/k}$
If , then the function is analytic in the annulus .

Theorem 8.2.2 (Laurent expansion of a function) Suppose that the function is analytic on the annulus $D=\{ z \in \mathbb{C}; \; r<\vert z\vert<R \}$ . Then has an expansion as a Laurent series in .

This series expansion of 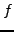is unique and its coefficients are given by:

$\displaystyle a_k= \frac {1}{2 \pi i} \int_C \frac {f(z)}{z^{k+1}} \; dz$

where 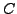is any simple smooth loop included in and enclosing the inner boundary circle of .

Corollary 8.2.3 (Generalization) Let be analytic in the annulus $D=\{ z \in \mathbb{C}; \; r<\vert z-z_0\vert<R \}$ . Then has a unique Laurent expansion $\underset{k=- \infty}{\overset{+ \infty}{\sum}} a_k (z-z_0)^k$ . The coefficients are given by the formula

$\displaystyle a_k= \frac {1}{2 \pi i} \int_C \frac {f(z)}{(z-z_0)^{k+1}} \; dz$

where is a any simple smooth loop included in 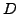and enclosing the inner boundary circle of .

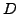Example 8.2.4

$\displaystyle \forall z \neq 0, \frac {(z+1)^3}{z} = \frac {1}{z} +3 +3z +z^2.$

Yes, this can happen: sometimes the Laurent expansion contains a finite numbers of terms (when?).

Example 8.2.5

$\displaystyle \frac {1}{z^2(1+z)} = \frac {1}{z^2} ( 1 - z + z^2 - z^3 + \dots ) = z^{-2} - z^{-1} + 1 - z + z^2 - \dots,$

This series converges for 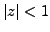$\vert z\vert<1$ . The convergence domain in the plane is the open unit disk centered at the origin; cf Fig 4(a).

**Figure 4:** Convergence domains of Laurent series.
$\begin{figure}\mbox{ \subfigure[]{{\epsfig{file=Laurent1.eps,height=3cm}}} \qquad \subfigure[]{{\epsfig{file=Laurent2.eps,height=3cm}}} }\end{figure}$

Example 8.2.6

$\displaystyle \frac {1}{z-2}$	$\displaystyle = \frac {1}{(z-1)-1} = \frac {\frac {1}{z-1}}{1- \frac {1}{z-1}}$
$\displaystyle \quad$	$\displaystyle = (z-1)^{-1} ( 1 + (z-1) + (z-1)^2 + (z-1)^3 + \dots )$
$\displaystyle \quad$	$\displaystyle = (z-1)^{-1} + 1 + (z-1) + (z-1)^2 + \dots.$

This series is convergent when 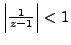$\left\vert \frac {1}{z-1} \right\vert <1$ , i.e. when 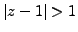$\vert z-1\vert>1$ (cf Fig 4(a).

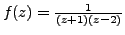
Example 8.2.7 Let $f(z)=\frac {1}{(z+1)(z-2)}$ . We wish to expand

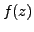
as a Laurent series convergent on an annulus.

We decompose 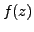as a sum of partial fractions:

$\displaystyle f(z)=\frac {1}{(z+1)(z-2)} = \frac 13 \cdot \frac {1}{z-2} - \frac 13 \cdot \frac {1}{z+1}$

Now, we expand both partial fractions as Laurent series about 0:

$\displaystyle \frac {1}{z+1} = 1- z + z^2 - z^3 + \dots + (-1)^n z^n + \dots$

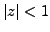This series is convergent for $\vert z\vert<1$ .
$\displaystyle \frac {1}{z-2}$ $\displaystyle = \frac {1}{z \left( 1-\frac 2z \right)}$

$\displaystyle \quad$ $\displaystyle = \frac 1z \cdot \left[ 1 + \frac 2z + \left( \frac 2z \right)^2 + \left( \frac 2z \right)^3 + \dots \right]$

$\displaystyle \quad$ $\displaystyle = z^{-1}+ 2 + 4z + 8z^2 + 16 z^3 + \dots$

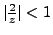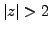This series is convergent for $\vert \frac 2z \vert<1$ ,i.e. $\vert z\vert>2$ .

The intersection of the two domains of convergence is empty, so we went in a wrong direction. Let us try in another way:

$\displaystyle \frac {1}{z+1}$ $\displaystyle = \frac {1}{z \left( 1 + \frac 1z \right)}$

$\displaystyle \quad$ $\displaystyle =\frac 1z \cdot \left[ 1 + \frac 1z + \left( \frac 1z \right)^2 +\left( \frac 1z \right)^3 +\dots \right]$

$\displaystyle \quad$ $\displaystyle = z^{-1}+1 + z + z^2 + z^3 + \dots$

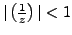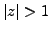This series is convergent for $\vert \left( \frac 1z \right) \vert < 1$ , i.e. $\vert z\vert>1$ .
$\displaystyle \frac {1}{z-2}$ $\displaystyle = \frac {-1}{2}\cdot \frac {1}{1- \frac z2}$

$\displaystyle \quad$ $\displaystyle = -\frac 12 \cdot \left[ 1 + \frac z2 + \left( \frac z2 \right)^2 + \left( \frac z2 \right)^3 + \dots \right]$

$\displaystyle \quad$ $\displaystyle = -\frac 12 \left[ 1 + \frac z2 + \frac 14 z^2 + \frac 18 z^3 + \dots \right]$

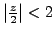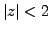This series is convergent for $\left\vert \frac z2 \right\vert <2$ , i.e. $\vert z\vert<2$ .

The intersection of these convergence domains is the annulus displayed on Fig 4(b). On this annulus, a Laurent series expansion of

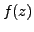
is:

$\displaystyle f(z)$	$\displaystyle = z^{-1}+1 + z + z^2 + z^3 + \dots -\frac 12 \left[ 1 + \frac z2 + \frac 14 z^2 + \frac 18 z^3 + \dots \right]$
$\displaystyle \quad$	$\displaystyle =z^{-1} + \frac 12 +z +\frac 12 z^2 -\frac {15}{16}z^3 + \dots .$

Discussion Center

Discuss/
Query
Papers/
Syllabus
Feedback/
Suggestion
Yahoo
Groups
Sirfdosti
Groups
Contact
Us

MEMBERS LOGIN

INTERVIEW EBOOK

Get 9,000+ Interview Questions & Answers in an eBook. Interview Question & Answer Guide

9,000+ Interview Questions
All Questions Answered
5 FREE Bonuses
Free Upgrades

GATE RESOURCES

Gate Books

Training Institutes

Gate FAQs

GATE BOOKS

Mechanical Engineeering Books

Robotics Automations Engineering Books

Civil Engineering Books

Chemical Engineering Books

Environmental Engineering Books

Electrical Engineering Books

Electronics Engineering Books

Information Technology Books

Software Engineering Books

GATE Preparation Books

Exciting Offers

GATE Exam, Gate 2009, Gate Papers, Gate Preparation & Related Pages GATE Overview \| GATE Eligibility \| Structure Of GATE \| GATE Training Institutes \| Colleges Providing M.Tech/M.E. \| GATE Score \| GATE Results \| PG with Scholarships \| Article On GATE \| GATE Forum \| GATE 2009 Exclusive \| GATE 2009 Syllabus \| GATE Organizing Institute \| Important Dates for GATE Exam \| How to Apply for GATE \| Discipline / Branch Codes \| GATE Syllabus for Aerospace Engineering \| GATE Syllabus for Agricultural Engineering \| GATE Syllabus for Architecture and Planning \| GATE Syllabus for Chemical Engineering \| GATE Syllabus for Chemistry \| GATE Syllabus for Civil Engineering \| GATE Syllabus for Computer Science / IT \| GATE Syllabus for Electronics and Communication Engineering \| GATE Syllabus for Engineering Sciences \| GATE Syllabus for Geology and Geophysics \| GATE Syllabus for Instrumentation Engineering \| GATE Syllabus for Life Sciences \| GATE Syllabus for Mathematics \| GATE Syllabus for Mechanical Engineering \| GATE Syllabus for Metallurgical Engineering \| GATE Syllabus for Mining Engineering \| GATE Syllabus for Physics \| GATE Syllabus for Production and Industrial Engineering \| GATE Syllabus for Pharmaceutical Sciences \| GATE Syllabus for Textile Engineering and Fibre Science \| GATE Preparation \| GATE Pattern \| GATE Tips & Tricks \| GATE Compare Evaluation \| GATE Sample Papers \| GATE Downloads \| Experts View on GATE \| CEED 2009 \| CEED 2009 Exam \| Eligibility for CEED Exam \| Application forms of CEED Exam \| Important Dates of CEED Exam \| Contact Address for CEED Exam \| CEED Examination Centres \| CEED Sample Papers \| Discuss GATE \| GATE Forum of OneStopGATE.com \| GATE Exam Cities \| Contact Details for GATE \| Bank Details for GATE \| GATE Miscellaneous Info \| GATE FAQs \| Advertisement on GATE \| Contact Us on OneStopGATE \|
Copyright © 2024. One Stop Gate.com. All rights reserved	Testimonials \|Link To Us \|Sitemap \|Privacy Policy \| Terms and Conditions\|About Us
Our Portals : Academic Tutorials \| Best eBooksworld \| Beyond Stats \| City Details \| Interview Questions \| India Job Forum \| Excellent Mobiles \| Free Bangalore \| Give Me The Code \| Gog Logo \| Free Classifieds \| Jobs Assist \| Interview Questions \| One Stop FAQs \| One Stop GATE \| One Stop GRE \| One Stop IAS \| One Stop MBA \| One Stop SAP \| One Stop Testing \| Web Hosting \| Quick Site Kit \| Sirf Dosti \| Source Codes World \| Tasty Food \| Tech Archive \| Software Testing Interview Questions \| Free Online Exams \| The Galz \| Top Masala \| Vyom \| Vyom eBooks \| Vyom International \| Vyom Links \| Vyoms \| Vyom World C Interview Questions \| C++ Interview Questions \| Send Free SMS \| Placement Papers \| SMS Jokes \| Cool Forwards \| Romantic Shayari