Limits and continuity.
Definition 3.1.1
Let
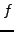
be a function of the complex variable
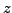
. The complex number
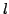
is called the limit of
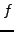
at
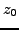
if
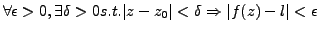 .
We denote:
Example 3.1.2
Let
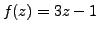
. We prove that
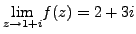
.
Let
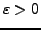 be given. We look for
be given. We look for
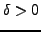 such that
such that
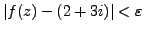 .
.
We take any
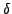 such that
such that
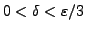 and we are done.
and we are done.
Definition 3.1.3
Let
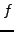
be a function defined on a domain
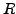
in
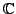
and let
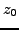
be an interior point of
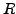
. The function
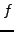
is continuous at
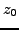
if
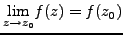
.
Formally this definition is identical to the corresponding definition in
Calculus. Thus we get easily the two following propositions:
Proposition 3.1.4
Let
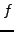 and
and
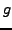 be two functions defined on a neighborhood of
be two functions defined on a neighborhood of
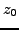 . We suppose that
. We suppose that
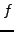 and
and
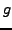 are continuous at
are continuous at
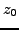 .
.
- (i)
-
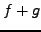 is continuous at
is continuous at
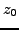 .
.
- (ii)
-
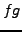 is continuous at
is continuous at
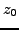 .
.
- (iii)
- If
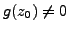 , then
, then
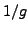 is continuous at
is continuous at
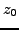 .
.
- (iv)
- If
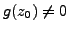 , then
, then
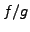 is continuous at
is continuous at
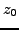 .
.
For a proof, we suggest to the reader to have a look at his/her course in
Calculus. The needed adaptation is merely to understand the absolute value here
as the absolute value of complex numbers instead of that of real numbers. The
same remark applies to Proposition 1.5.
Proposition 3.1.5
Let
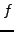 be a function defined on a neighborhood of
be a function defined on a neighborhood of
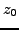 and let
and let
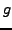 be a function defined on a neighborhood of
be a function defined on a neighborhood of
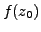 . If
. If
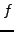 is continuous at
is continuous at
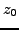 and if
and if
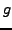 is continuous at
is continuous at
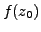 , then
, then
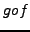 is continuous at
is continuous at
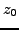 .
.
Recall that a polynomial function is a function of the form
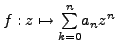 , where all the
, where all the
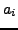 are given complex numbers and
are given complex numbers and
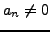 . We apply the two first properties of Proposition 1.4
to prove Corollary 1.6.
. We apply the two first properties of Proposition 1.4
to prove Corollary 1.6.
Corollary 3.1.6
A polynomial function is continuous on the whole of
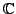 .
.
Recall now that a rational function is the quotient of two polynomial
functions. Applying the last property of Proposition 1.4
to prove Corollary 1.6,
we prove Corollary 1.7.
Corollary 3.1.7
A rational function is continuous at every point of its domain of
definition.
Example 3.1.8
The function
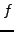
such that
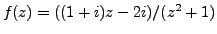
is continuous on
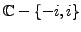
.
|