The logarithm of a complex number.
Definition 4.4.1
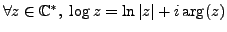
,
|
where
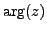
is defined up to an additive multiple of 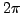
.
We denote
Log the principal value of
the principal value of 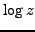 ,
i.e. the value corresponding to the principal value
,
i.e. the value corresponding to the principal value
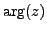 of
of
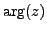 (recall that
(recall that
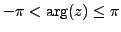 ).
).
Proposition 4.4.5
The logarithmic function is analytic on its domain.
For a proof, use Cauchy-Riemann equations (v.s. 3).
Example 4.4.7
The proof is simple: let 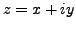 , where
, where
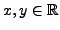 . Then we have:
. Then we have:
and
Proposition 4.8 means that the 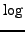 function is not exactly the inverse of the
complex exponential function in basis
function is not exactly the inverse of the
complex exponential function in basis 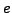 .
.
|