Polar form
Let
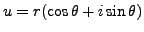 , where
, where
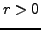 and
and
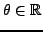 . .
The precise meaning of the last equation, namely of
is that there exist exactly
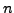 distinct
distinct
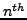 roots for any non zero complex number
roots for any non zero complex number
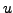 . You can check this by the following way: let
. You can check this by the following way: let
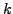 increase from 0 to
increase from 0 to
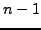 , you have distinct numbers. From
, you have distinct numbers. From
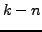 and further on, you get the same complex numbers again (you only added a
multiple of
and further on, you get the same complex numbers again (you only added a
multiple of
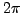 to the argument...).
to the argument...).
Example 1.5.2
Find the cubic roots of
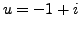
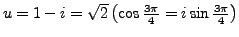 . Thus:
. Thus:
The cubic roots of
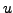 are:
are:
Example 1.5.3
Find the cubic roots of
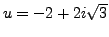
.
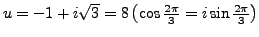 . Thus:
. Thus:
The cubic roots of
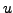 are:
are:
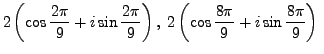 and
and
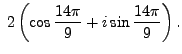 |
|