Polar form.
We denote by
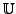 the set of all complex numbers whose absolute value is equal to 1.
the set of all complex numbers whose absolute value is equal to 1.
For example,
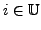 and
and
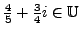 , but
, but
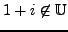 .
.
The image of
 in the Cauchy-Argand plane is the unit circle: if
in the Cauchy-Argand plane is the unit circle: if
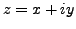 , with real
, with real
 , then
, then
 if,
and only if if,
and only if
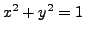 .
.
Proposition 1.3.1
Let
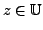 ; then ; then
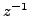 exists and is an element of
exists and is an element of
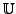 .
.
We leave the proof to the reader; use Corollary 1.18.
Proposition 1.3.2
For any
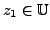 and
and
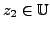 , we have
, we have
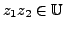 .
.
Proof. For any
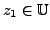
and
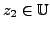
, we have:
whence
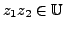 .
.
And now we will see how complex numbers are tied with trigonometry.
Theorem 1.3.3
Let
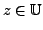 .
There exists a real number .
There exists a real number
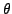 such that
such that
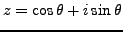 .
.
Proof. Denote
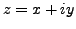
, where
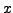
and
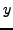
are real numbers. Then
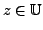 if,
and only if,
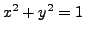
, i.e. the image of
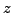
in the complex plane is a point on the unit-circle. For each point on the
unit-circle, there exist a real number
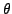
such that the coordinates of this point are
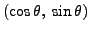
, whence the result.
Definition 1.3.4
The number
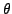
is called an argument of
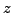
and is denoted
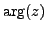
.
Note that this argument is defined up to an additional
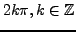 .
.
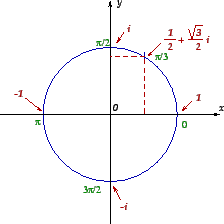
In Fig 5,
a value of the argument of the complex number corresponding to a point is
diplayed in green.
Figure 5: The unit circle in
Cauchy-Argand plane.
 |
We can now generalize this to any non zero complex number. First note that
for any
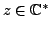 , we have
, we have
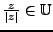 , as the following holds:
, as the following holds:
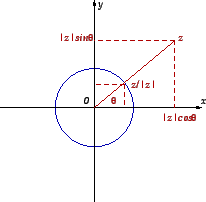
Definition 1.3.6
For any
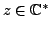
,
Figure 6: The trigonometric
form of a non zero complex number.
 |
The following proposition is easy to understand. It explains the specific
role of the coordinate axes when representing complex numbers in the
Cauchy-Argand plane.
Figure 7: Particular cases.
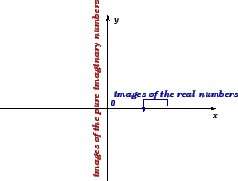 |
Proof. Let
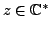
; denote
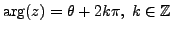
. Then:
(i)
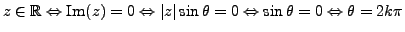 .
.
(ii)
Please do it yourself.
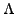
|