Polynomial equations of higher degree.
The Fundamental Theorem of Algebra,
which states that if
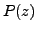is a non constant polynomial over
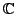, then
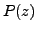has a root.
Here are some examples of applications, based on the following theorems.
Recall that a root of a polynomial
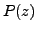is a number
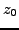such that
.
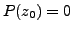Theorem 1.7.1
Let
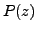be a polynomial in one complex variable
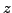, with complex coefficients. The complex number
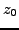is a root of
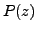if, and only if, there exists a polynomial
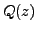such that
.
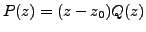Proof. We denote
where
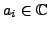
, for every
.
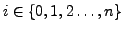
The ``if'' part is trivial.
For the ``only if'' part, suppose that
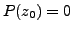. Then we have:
By section section algebraic form, all the terms
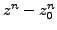
have a common factor
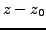
, whence the result.
Theorem 1.7.3
Let
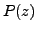be a polynomial in one complex variable
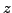, with real coefficients. If the complex number
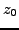is a root of
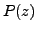, then its complex conjugate
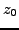is also a root of
.
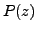The following corollary can be obtained either as a consequence of the
Fundamental Theorem of Algebra thm fundamental, or as a consequence of the
Intermediate Value Theorem in Calculus.
Corollary 1.7.5
A polynomial of odd degree over the reals has at least one real root.
Proof. Let
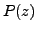
be a polynomial of odd degree
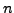
with real coefficients. By the Fundamental Theorem of Algebra, it has
exactly
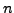
complex roots, counted with multiplicity. As the coefficients are real, the
roots are organized by pairs of conjugate complex numbers. Suppose that
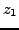
is a root of
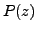
. If
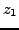
is real, we are done; otherwise,
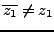
is another root of
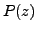
. Take now another root
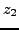
. If If
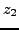
is real, we are done; otherwise,
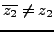
is another root of
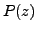
. It is not important to know whether
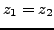
or
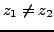
. Iterate this process until we discover the first (maybe the only) real
root of
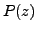
. As roots are organized by pairs, the maximum number of roots (either
distinct or not) which can be involved in the process is even, and it is
equal to
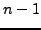
. The last root
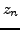
cannot be equal to a previous one, as in such a case its conjugate should
appear also now, and this is impossible. Thus,
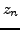
must be equal to its conjugate, i.e.
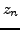
is a real number.
Remark 1.7.6
A consequence of these theorems is a method for factorizing polynomials of
higher degree in one real variable, despite the fact that they have no real
root. Let us see an example.
Let
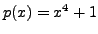. This polynomial has no real root, but it has complex conjugate roots:
Moreover, by one of the methods described in subsection 6 ,
we have:
and
It follows:
Thus:
|
, getting two solutions, namely 
![$\displaystyle \forall z \in \mathbb{C}, \; z^2+i = \left[ z- \frac {\sqrt{2}}{2...
...qrt{2}}{2} \right] \left[ z+ \frac {\sqrt{2}}{2}- i \frac {\sqrt{2}}{2} \right]$](/images/maths/complex-analysis/polynomial/img395.png)
![$\displaystyle \forall z \in \mathbb{C}, \; z^2-i = \left[ z- \frac {\sqrt{2}}{2...
...qrt{2}}{2} \right] \left[ z+ \frac {\sqrt{2}}{2}+ i \frac {\sqrt{2}}{2} \right]$](/images/maths/complex-analysis/polynomial/img396.png)
![$\displaystyle = \left[ z- \frac {\sqrt{2}}{2}+ i \frac {\sqrt{2}}{2} \right] \l...
...qrt{2}}{2} \right] \left[ z+ \frac {\sqrt{2}}{2}+ i \frac {\sqrt{2}}{2} \right]$](/images/maths/complex-analysis/polynomial/img398.png)
![$\displaystyle = \underbrace{ \left[ z- \frac {\sqrt{2}}{2}+ i \frac {\sqrt{2}}{...
...eft[ z+ \frac {\sqrt{2}}{2}+ i \frac {\sqrt{2}}{2} \right] }_{=z^2+z\sqrt{2}+1}$](/images/maths/complex-analysis/polynomial/img399.png)
