Residues.
Let
be a function analytic on a simple Jordan curve
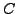and at all the interior points, excepted at
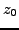. The residue of
at
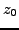, denoted Res[
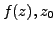] is the complex number;
Res![$\displaystyle [f(z),z_0] = \frac {1}{2 \pi i} \int_C f(z) \; dz$](/images/maths/complex-analysis/residues/img1159.png) |
|
Theorem 9.1.1
The residue of
at
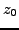is the coefficient
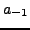in the Laurent series expansion of
in an annulus
.
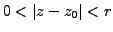Example 9.1.2
Compute the integral
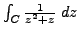
, where
.
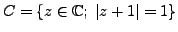
We compute a Laurent series expansion for
which is convergent on an annulus centered at -1.
Therefore
.
|
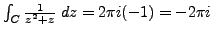![$\displaystyle [f(z),z_0]= \underset{z \rightarrow z_0}{\text{lim}} (z-z_0)f(z).$](/images/maths/complex-analysis/residues/img1170.png){kind=small}
![$\displaystyle [f(z),z_0]= \underset{z \rightarrow z_0}{\text{lim}} \frac {d}{dz}((z-z_0)^2f(z)).$](/images/maths/complex-analysis/residues/img1171.png)
![$\displaystyle [f(z),z_0]= \underset{z \rightarrow z_0}{\text{lim}} \frac {1}{(n-1)!} \frac {d^{n-1}}{dz^{n-1}}((z-z_0)^nf(z)).$](/images/maths/complex-analysis/residues/img1172.png)
![$\displaystyle [f(z),z_0]= \frac {g(z_0)}{h'(z_0)}$](/images/maths/complex-analysis/residues/img1174.png)
