Roots of unity
Definition 1.5.4
Let
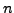
be a natural number such that
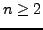
. A complex number

such that
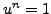
is called an
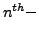
root of unity.
By the method of subsection
5.1,
we compute all the
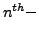 roots of unity:
roots of unity:
For
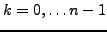 , we have the following roots:
, we have the following roots:
The images in Gauss-Argand plane of the
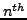 roots of unity are the vertices of a regular polygone inscribed in the unit
circle.
roots of unity are the vertices of a regular polygone inscribed in the unit
circle.
By De Moivre's formula De Moivre's formula, the following holds:
An immediate consequence is as follows:
Proposition
1.5.7
Let
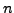 be a natural number such that
be a natural number such that
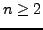 . The sum of all
. The sum of all
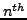 roots of unity is equal to 0.
roots of unity is equal to 0.
Proof
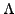
Now, let us see a nice application of these roots of unity.
Proposition
1.5.8
Let
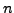 be a natural number such that
be a natural number such that
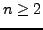 . Suppose that
. Suppose that

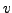 are two complex numbers such that
are two complex numbers such that
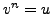 . Then we obtain all the
. Then we obtain all the
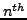 roots of
roots of
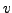 by separate multiplication of
by separate multiplication of
 by all the
by all the
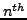 roots of unity.
roots of unity.
Example 1.5.9
Squarring twice, we obtain
By Proposition
5.8, the
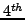
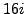 are given by:
are given by:
An additional result of this example is the following: compute polar
forms for the
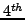 roots of
roots of
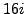 . Theses roots have arguments
. Theses roots have arguments
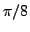 ,
,
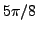 ,
,
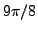 and
and
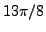 . They fit exactly the order of the roots given above.
. They fit exactly the order of the roots given above.
|