Looking for GATE Preparation Material? Join & Get here now!

** Gate 2013 Question Papers.. ** CEED 2013 Results.. ** Gate 2013 Question Papers With Solutions.. ** GATE 2013 CUT-OFFs.. ** GATE 2013 Results.. **

Series with non negative real terms

Series with non negative real terms.

We recall here the most important tests for convergence, which will be useful in the next sections. There exist other tests; the interested reader can see them in the Calculus Tutorial.

$\mathbb{C}$

Proposition 7.1.7 (Direct Comparison) Let $\underset{n=0}{\overset{+\infty }{\sum}} u_n$ be a series of real numbers, such that $\forall n \in \mathbb{N}, u_n \geq 0$ .

Suppose that there exists a convergent series $\underset{n=0}{\overset{+\infty }{\sum}} v_n$ such that, for a given natural number , $n \geq N \Longrightarrow 0 \leq u_n \leq v_n$ . Then the series $\underset{n=0}{\overset{+\infty }{\sum}} u_n$ is convergent.
Suppose that there exists a divergent series $\underset{n=0}{\overset{+\infty }{\sum}} w_n$ such that, for a given natural number , $n \geq N \Longrightarrow 0 \leq w_n \leq u_n$ . then the series $\underset{n=0}{\overset{+\infty }{\sum}} u_n$ is divergent.

Example 7.1.8 Consider the series $\underset{n=0}{\overset{+\infty }{\sum}} e^{-n^2}$ . This is a series with positive terms.

For $n \geq 1$ , we have $e^{-n^2} \leq e^{-n}$ . By the integral test (consult the Calculus Tutorial), the series $\underset{n=0}{\overset{+\infty }{\sum}} e^{-n}$ is convergent; thus the given series $\underset{n=0}{\overset{+\infty }{\sum}} e^{-n^2}$ is convergent.

Proposition 7.1.9 (Limit Comparison) Let $\underset{n=0}{\overset{+\infty }{\sum}} u_n$ and $\underset{n=0}{\overset{+\infty }{\sum}} v_n$ be two series of real numbers, such that $\forall n \in \mathbb{N}, u_n \geq 0$ and $v_n \geq 0$ .

If there exists a positive real number L such that $\underset{n \rightarrow + \infty }{\text{lim}} \frac {u_n}{v_n} = L$ , then the two series either are both convergent or are both divergent.
If $\underset{n \rightarrow + \infty }{\text{lim}} \frac {u_n}{v_n} =0$ and $\underset{n=0}{\overset{+\infty }{\sum}} v_n$ is convergent, then $\underset{n=0}{\overset{+\infty }{\sum}} u_n$ is convergent.
If $\underset{n \rightarrow + \infty }{\text{lim}} \frac {u_n}{v_n} = + \infty$ and $\underset{n=0}{\overset{+\infty }{\sum}} v_n$ is divergent, then $\underset{n=0}{\overset{+\infty }{\sum}} u_n$ is divergent.

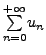
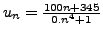
Example 7.1.10 Consider the series $\underset{n=0}{\overset{+\infty }{\sum}} u_n$ , where $u_n=\frac {100n+345}{0.n^4+1}$ . For arbitrarily large

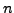
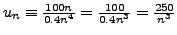
, we have $u_n \equiv \frac {100n}{0.4n^4}=\frac {100}{0.4n^3} = \frac {250}{n^3}$ .

Take 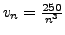$v_n= \frac {250}{n^3}$ . Then:

$\displaystyle \frac {u_n}{v_n} = \frac {\frac {100n+345}{0.n^4+1}}{\frac {250}{n^3}} =\frac {.5n^3(20n+69)}{n^4+2.5}$

Thus:

$\displaystyle \underset{n \rightarrow + \infty }{\text{lim}} \frac {u_n}{v_n} =... ...{n^4+2.5} = \underset{n \rightarrow + \infty }{\text{lim}} \frac{10n^4}{n^4}=10$

The series 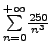$\underset{n=0}{\overset{+\infty }{\sum}} \frac {250}{n^3}$ is a Riemann 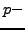series with 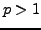, thus it is convergent; therefore, by Thm 1.9, the given series is convergent.

Proposition 7.1.11 (Ratio Test; d'Alembert's Test) Let $\underset{n=0}{\overset{+\infty }{\sum}} u_n$ such that $\forall n \in \mathbb{N}, u_n \geq 0$ . Suppose that:

$\displaystyle \underset{n \rightarrow + \infty }{\text{lim}} \frac {u_{n+1}}{u_n} = L.$

Then:

If , the series is convergent.
If or $L=+\infty$ , the series is divergent.
If , the test gives no conclusion.

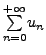
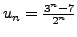
Example 7.1.12 Take the series $\underset{n=0}{\overset{+\infty }{\sum}} u_n$ with general term $u_n= \frac {3^n -7}{2^n}$ . We have:

$\displaystyle \frac {u_{n+1}}{u_n}= \frac {\frac {3^{n+1} -7}{2^+{n+1}}}{\frac ... ...{3^n -7} \cdot \frac{2^n}{2^+{n+1}} =\frac 12 \cdot \frac {3^{n+1} -7}{3^n -7}.$

Thus:

$\displaystyle \underset{n \rightarrow + \infty }{\text{lim}} \frac {u_{n+1}}{u_... ... \underset{n \rightarrow + \infty }{\text{lim}} \frac {3^{n+1}}{3^n} =\frac 32.$

As this limit is more than 1, the given series is divergent.

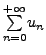
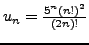
Example 7.1.13 The series $\underset{n=0}{\overset{+\infty }{\sum}} u_n$ with general term $u_n= \frac{5^n (n!)^2}{(2n)!}$ is given. We have:

$\displaystyle \frac {u_{n+1}}{u_n}= \frac { \frac{5^{n+1} [(n+1)!]^2}{[2(n+1)])!}}{ \frac{5^n (n!)^2}{(2n)!}} =\frac {5 (n+1)}{2(2n+1)}$

Thus:

$\displaystyle \underset{n \rightarrow + \infty }{\text{lim}} \frac {u_{n+1}}{u_... ... \underset{n \rightarrow + \infty }{\text{lim}} \frac {n+1}{2(2n+1)} = \frac 54$

Discussion Center

Discuss/
Query
Papers/
Syllabus
Feedback/
Suggestion
Yahoo
Groups
Sirfdosti
Groups
Contact
Us

MEMBERS LOGIN

INTERVIEW EBOOK

Get 9,000+ Interview Questions & Answers in an eBook. Interview Question & Answer Guide

9,000+ Interview Questions
All Questions Answered
5 FREE Bonuses
Free Upgrades

GATE RESOURCES

Gate Books

Training Institutes

Gate FAQs

GATE BOOKS

Mechanical Engineeering Books

Robotics Automations Engineering Books

Civil Engineering Books

Chemical Engineering Books

Environmental Engineering Books

Electrical Engineering Books

Electronics Engineering Books

Information Technology Books

Software Engineering Books

GATE Preparation Books

Exciting Offers

GATE Exam, Gate 2009, Gate Papers, Gate Preparation & Related Pages GATE Overview \| GATE Eligibility \| Structure Of GATE \| GATE Training Institutes \| Colleges Providing M.Tech/M.E. \| GATE Score \| GATE Results \| PG with Scholarships \| Article On GATE \| GATE Forum \| GATE 2009 Exclusive \| GATE 2009 Syllabus \| GATE Organizing Institute \| Important Dates for GATE Exam \| How to Apply for GATE \| Discipline / Branch Codes \| GATE Syllabus for Aerospace Engineering \| GATE Syllabus for Agricultural Engineering \| GATE Syllabus for Architecture and Planning \| GATE Syllabus for Chemical Engineering \| GATE Syllabus for Chemistry \| GATE Syllabus for Civil Engineering \| GATE Syllabus for Computer Science / IT \| GATE Syllabus for Electronics and Communication Engineering \| GATE Syllabus for Engineering Sciences \| GATE Syllabus for Geology and Geophysics \| GATE Syllabus for Instrumentation Engineering \| GATE Syllabus for Life Sciences \| GATE Syllabus for Mathematics \| GATE Syllabus for Mechanical Engineering \| GATE Syllabus for Metallurgical Engineering \| GATE Syllabus for Mining Engineering \| GATE Syllabus for Physics \| GATE Syllabus for Production and Industrial Engineering \| GATE Syllabus for Pharmaceutical Sciences \| GATE Syllabus for Textile Engineering and Fibre Science \| GATE Preparation \| GATE Pattern \| GATE Tips & Tricks \| GATE Compare Evaluation \| GATE Sample Papers \| GATE Downloads \| Experts View on GATE \| CEED 2009 \| CEED 2009 Exam \| Eligibility for CEED Exam \| Application forms of CEED Exam \| Important Dates of CEED Exam \| Contact Address for CEED Exam \| CEED Examination Centres \| CEED Sample Papers \| Discuss GATE \| GATE Forum of OneStopGATE.com \| GATE Exam Cities \| Contact Details for GATE \| Bank Details for GATE \| GATE Miscellaneous Info \| GATE FAQs \| Advertisement on GATE \| Contact Us on OneStopGATE \|
Copyright © 2024. One Stop Gate.com. All rights reserved	Testimonials \|Link To Us \|Sitemap \|Privacy Policy \| Terms and Conditions\|About Us
Our Portals : Academic Tutorials \| Best eBooksworld \| Beyond Stats \| City Details \| Interview Questions \| India Job Forum \| Excellent Mobiles \| Free Bangalore \| Give Me The Code \| Gog Logo \| Free Classifieds \| Jobs Assist \| Interview Questions \| One Stop FAQs \| One Stop GATE \| One Stop GRE \| One Stop IAS \| One Stop MBA \| One Stop SAP \| One Stop Testing \| Web Hosting \| Quick Site Kit \| Sirf Dosti \| Source Codes World \| Tasty Food \| Tech Archive \| Software Testing Interview Questions \| Free Online Exams \| The Galz \| Top Masala \| Vyom \| Vyom eBooks \| Vyom International \| Vyom Links \| Vyoms \| Vyom World C Interview Questions \| C++ Interview Questions \| Send Free SMS \| Placement Papers \| SMS Jokes \| Cool Forwards \| Romantic Shayari