Uniform convergence

Uniform convergence.

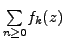
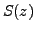
Definition 7.3.1   The series is uniformly convergent to in a domain

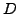
if

 

where 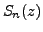denotes the 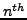partial sum of the series.

Note that here 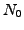depends on 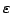only, not on the point .

Theorem 7.3.2 (Weierstrass)   We use the notations of the definition. Let be a convergent series of positive real numbers. Suppose that for any , is an upper bound for on . Then the series converges absolutely and uniformely on .

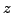Theorem 7.3.3   Suppose that the series 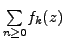converges uniformely to 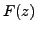on 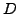and that the function 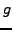is bounded on 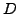. Then the series 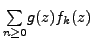is uniformly convergent on 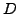and its sum is equal to .

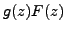Theorem 7.3.4   Suppose that the series 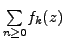converges uniformely to 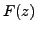on 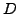. If every function 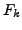is continuous on 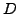, then the sum 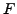is continuous on .

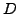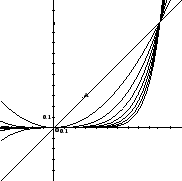
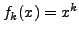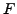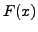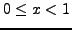A famous example of a non-uniformly convergent sequence of functions is given in Calculus: take oj the interval . The limit of this sequence is the function such that for and 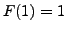. As this limit is non continuous at 1, the sequence is not uniformly convergent (see Fig. 1).

Figure 1: Non uniform convergence of a sequence of functions.

For the series 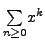, it is defined on , but convergent only on .

Theorem 7.3.5 (term-by-term integration)   Suppose that the series converges uniformly to on the domain and that every is continuous on . Denote by a Jordan curve in . Then, we have:

 

 

Corollary 7.3.6 (analyticity of the sum)   Suppose that the series converges uniformely on the domain and that every is analytic on . Then the sum of the series is analytic on .

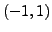As a consequence, we have that power series converge uniformly on their open domain of convergence .

Theorem 7.3.7 (term-by-term differentiation)   Suppose that the series converges uniformely on the domain and denote its sum by . If all the functions are analytic on , then at any interior point of , we have: