Banach Space

A Banach space is a complete vector space 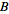with a norm 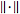. Two norms 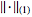and 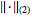are called equivalent if they give the same topology, which is equivalent to the existence of constants 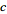and 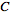such that

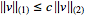(1)

and

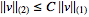(2)

hold for all .

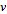In the finite-dimensional case, all norms are equivalent. An infinite-dimensional space can have many different norms.

A basic example is 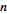-dimensional Euclidean space with the Euclidean norm. Usually, the notion of Banach space is only used in the infinite dimensional setting, typically as a vector space of functions. For example, the set of continuous functions on closed interval of the real line with the norm of a function 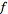given by

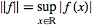(3)

is a Banach space, where 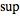denotes the supremum.

On the other hand, the set of continuous functions on the unit interval with the norm of a function 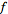given by

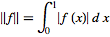(4)

is not a Banach space because it is not complete. For instance, the Cauchy sequence of functions

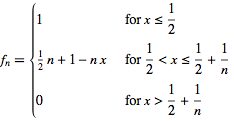(5)

does not converge to a continuous function.

Hilbert spaces with their norm given by the inner product are examples of Banach spaces. While a Hilbert space is always a Banach space, the converse need not hold. Therefore, it is possible for a Banach space not to have a norm given by an inner product. For instance, the supremum norm cannot be given by an inner product.

Renteln and Dundes (2005) give the following (bad) mathematical joke about Banach spaces:

Q: What's yellow, linear, normed, and complete? A: A Bananach space.