A Hilbert space is a
vector
space
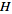 with an
inner
product
with an
inner
product
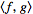 such that the
norm defined by
such that the
norm defined by
turns
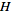 into a
complete metric space. If the
metric
defined by the
norm is
not
complete, then
into a
complete metric space. If the
metric
defined by the
norm is
not
complete, then
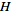 is instead known as an
inner product space.
is instead known as an
inner product space.
Examples of
finite-dimensional
Hilbert spaces include
1. The
real
numbers
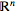 with
with
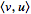 the vector
dot
product of
the vector
dot
product of
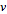 and
and
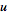 . .
2. The
complex numbers
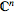 with
with
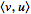 the vector
dot
product of
the vector
dot
product of
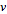 and the
complex conjugate of
and the
complex conjugate of
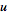 . .
An example of an
infinite-dimensional
Hilbert space is
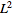 ,
the set of
all
functions ,
the set of
all
functions
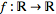 such that the
integral
of
such that the
integral
of
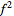 over the whole
real line
is finite.
In this case, the
inner
product is
over the whole
real line
is finite.
In this case, the
inner
product is
A Hilbert space is always a
Banach
space, but the converse need not hold.
A (small) joke told in the hallways of MIT ran, "Do you know
Hilbert? No? Then what are you doing in his space?" (S. A. Vaughn, pers. comm.,
Jul. 31, 2005).
|