Unbounded 2-var LP's
In the LP's considered above, the feasible region (if not empty) was a
bounded area of the
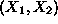-plane. For this kind of problems it is obvious that all values of the LP
objective function (and therefore the optimal) are bounded. Consider however the
following LP:
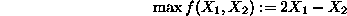
s.t.
The feasible region and the direction of improvement for the isoprofit lines
for this problem are given in Figure6
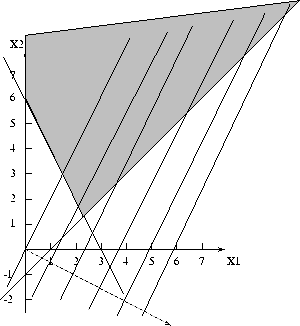
Figure 6: An unbounded LP
It is easy to see that the feasible region of this problem is unbounded, and
furthermore, the orientation of the isoprofit lines is such that no matter how
far we ``slide'' these lines in the direction of increasing the objective
function, they will always share some points with the feasible region.
Therefore, this is an example of a (2-var) LP whose objective function can take
arbitrarily large values. Such an LP is characterized as unbounded.
Notice, however, that even though an unbounded feasible region is a necessary
condition for an LP to be unbounded, it is not sufficient; to convince yourself,
try to graphically identify the optimal solution for the above LP in the case
that the objective function is changed to:
.
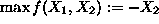Summarizing the above discussion, we have shown that a 2-var LP can either
- have a unique optimal solution which corresponds to a
``corner'' point of the feasible region, or
- have many optimal solutions that correspond to an entire
``edge'' of the feasible region, or
- be unbounded, or
- be infeasible.
In the next section, we generalize this geometrical description of the LP
solution space for the n-var LP case, and we provide a brief (informal)
derivation of the Fundamental Theorem of Linear Programming. The latter
states that if an LP has a bounded optimal solution, then it must have one which
is an extreme point of its feasible region. The Simplex algorithm to be
discussed in the last section of this set of notes essentially exploits this
fundamental result to reduce the space to be searched for an optimal solution.
Finally, you can actively try the graphical approach to the solution of
2-var LP's discussed above, by using the code developed by the group of
Professors Ken Goldberg and Ilan Adler, at the University of
Berkeley, Dept. of Industrial Engineering and Operations Research. Notice
that the problem formulation uses a "minimization" objective, and all
variables are considered to be "urs". Therefore, (i) any maximization
problem must be turned into a minimization one (can you think of an easy way?),
and (ii) all sign restrictions must be introduced in the formulation explicitly.
Other than that, the software is self-explanatory.
|
