Polytope Convexity and Extreme Points
In this paragraph we show that polytopes are convex sets. This
property is important for eventually proving the Fundamental Theorem of LP. A
set of points S in the n-dim space is convex, if the line
segment connecting any two points
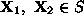, belongs completely in S. According to the previous mathematical
definition of line segments, this definition of convexity is mathematically
expressed as:
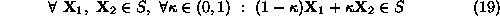
Figure8
depicts the concept.
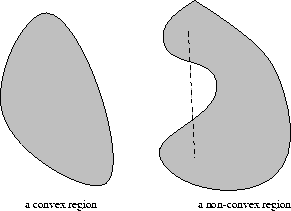
Figure 8: Convex sets
To show that a polytope is a convex set, we first establish that the solution
space of any linear constraint (i.e., hyperplanes and half-spaces) is a convex
set. Since a polytope is the intersection of a number of hyperplanes
and half-spaces, the convexity of the latter directly implies the convexity of
the polytope (i.e., a line segment belonging to each defining hyperplane and/or
half-space will also belong to the polytope).
To establish the convexity of the feasible region of a linear constraint,
let's consider the constraint:
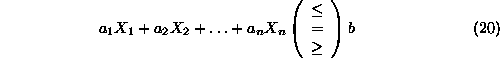
and two points
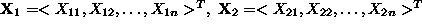satisfying it. Then, for any
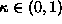, we have:
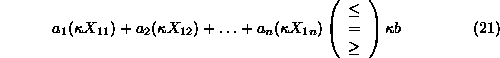
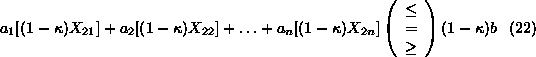
Adding Equations21
and22,
we get:
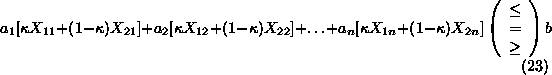
i.e., point
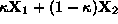belongs in the solution space of the constraint.
A last concept that we must define before the statement of the
Fundamental Theorem of LP, is that of the extreme point of a
convex set. Given a convex set S, point
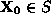is an extreme point, if each line segment that lies completely in S
and contains point
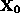, has
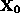as an end point of the line segment. Mathematically,
|
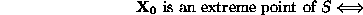
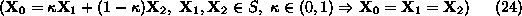
