A prototype LP problem:
Consider a company which produces two types of products
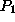 and
and
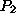 . Production of these products is supported by two workstations
. Production of these products is supported by two workstations
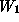
and
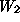 , with each station visited by both product types. If workstation
, with each station visited by both product types. If workstation
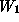 is dedicated completely to the production of product type
is dedicated completely to the production of product type
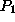 , it can process 40 units per day, while if it is dedicated to the production of
product
, it can process 40 units per day, while if it is dedicated to the production of
product
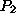 , it can process 60 units per day. Similarly, workstation
, it can process 60 units per day. Similarly, workstation
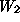 can produce daily 50 units of product
can produce daily 50 units of product
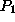 and 50 units of product
and 50 units of product
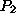 , assuming that it is dedicated completely to the production of the
corresponding product. If the company's profit by disposing one unit of product
, assuming that it is dedicated completely to the production of the
corresponding product. If the company's profit by disposing one unit of product
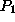 is $200 and that of disposing one unit of
is $200 and that of disposing one unit of
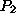 is $400, and assumning that the company can dispose its entire production, how
many units of each product should the company produce on a daily basis to
maximize its profit?
is $400, and assumning that the company can dispose its entire production, how
many units of each product should the company produce on a daily basis to
maximize its profit?
Solution: First notice that this problem is an optimization
problem. Our objective is to maximize the company's profit,
which under the problem assumptions, is equivalent to maximizing the company's
daily profit. Furthermore, we are going to maximize the company profit
by adjusting the levels of the daily production for the two items
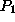 and
and
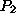 . Therefore, these daily production levels are the control/decision factors, the
values of which we are called to determine. In the analytical formulation of the
problem, the role of these factors is captured by modeling them as the problem
decision variables:
. Therefore, these daily production levels are the control/decision factors, the
values of which we are called to determine. In the analytical formulation of the
problem, the role of these factors is captured by modeling them as the problem
decision variables:
-
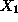 := number of units of product
:= number of units of product
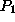 to be produced daily
to be produced daily
-
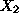 := number of units of product
:= number of units of product
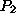 to be produced daily
to be produced daily
In the light of the above discussion, the problem objective can be expressed
analytically as:
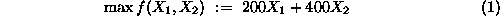
Equation1
will be called the objective function of the problem, and the
coefficients 200 and 400 which multiply the decision variables in it, will be
called the objective function coefficients.
Furthermore, any decision regarding the daily production levels for items
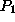 and
and
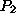 in order to be realizable in the company's operation context must observe the
production capacity of the two worksations
in order to be realizable in the company's operation context must observe the
production capacity of the two worksations
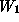 and
and
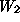 . Hence, our next step in the problem formulation seeks to introduce these
technological constraints in it. Let's focus first on the constraint which
expresses the finite production capacity of workstation
. Hence, our next step in the problem formulation seeks to introduce these
technological constraints in it. Let's focus first on the constraint which
expresses the finite production capacity of workstation
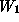 . Regarding this constraint, we know that one day's work dedicated to the
production of item
. Regarding this constraint, we know that one day's work dedicated to the
production of item
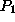 can result in 40 units of that item, while the same period dedicated to the
production of item
can result in 40 units of that item, while the same period dedicated to the
production of item
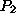 will provide 60 units of it. Assuming that production of one unit of product
type
will provide 60 units of it. Assuming that production of one unit of product
type
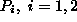 , requires a constant amount of processing time
, requires a constant amount of processing time
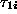 at workstation
at workstation
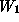 , it follows that:
, it follows that:
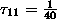 and
and
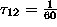 . Under the further assumption that the combined production of both items
has no side-effects, i.e., does not impose any additional requirements for
production capacity of workstation
. Under the further assumption that the combined production of both items
has no side-effects, i.e., does not impose any additional requirements for
production capacity of workstation
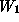 (e.g., zero set-up times), the total capacity (in terms of time length)
required for producing
(e.g., zero set-up times), the total capacity (in terms of time length)
required for producing
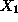 units of product
units of product
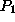 and
and
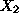 units of product
units of product
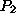 is equal to
is equal to
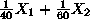 . Hence, the technological constraint imposing the condition that our total
daily processing requirements for workstation
. Hence, the technological constraint imposing the condition that our total
daily processing requirements for workstation
 should not exceed its production capacity, is analytically expressed by:
should not exceed its production capacity, is analytically expressed by:
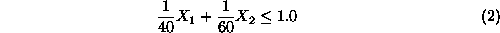
Notice that in Equation2
time is measured in days.
Following the same line of reasoning (and under similar assumptions), the
constraint expressing the finite processing capacity of workstation
 is given by:
is given by:
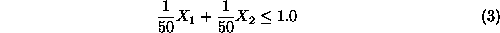
Constraints2
and3 are
known as the technological constraints of the problem. In particular,
the coefficients of the variables
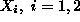 in them,
in them,
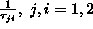 , are known as the technological coefficients of the problem
formulation, while the values on the right-hand-side of the two inequalities
define the right-hand side (rhs) vector of the constraints.
, are known as the technological coefficients of the problem
formulation, while the values on the right-hand-side of the two inequalities
define the right-hand side (rhs) vector of the constraints.
Finally, to the above constraints we must add the requirement that any
permissible value for variables
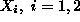 must be nonnegative, i.e.,
must be nonnegative, i.e.,
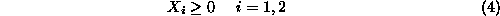
since these values express production levels. These constraints are known as
the variable sign restrictions.
Combining Equations1
to4, the
analytical formulation of our problem is as follows:
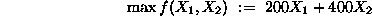
s.t.


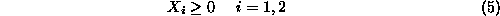
|

