The basic Simplex iteration through an
example:
Consider our prototype LP in standard form, repeated below for convenience:
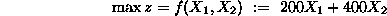
s.t.
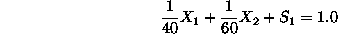
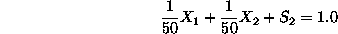
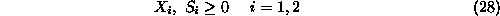
Finding an initial bfs To start the Simplex algorithm on this problem,
we need to identify an initial bfs. For this particular problem, a bfs will have
two basic variables, since we have two technological constraints. Taking a
closer look to the structure of these constraints in Equation28,
it can be seen that a convenient selection is
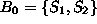, where
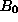denotes the set of basic variables (basis). Indeed, setting
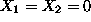, we readily obtain,
.
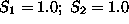The above easy computation of the values of the basic variables resulted from
the fact that each of these variables could be associated with one and only one
constraint. More specifically, (i) each of these variables appeared in only one
constraint, (ii) the coefficient of the variable in that constraint was equal to
1.0, and (iii) any pair of basic variables showed up in different constraints.
An LP the constraints of which satisfy these three properties with respect to a
certain basis, is said to be in canonical form with respect to that
basis.
On the other hand, thefeasiblity of the above basis,
,
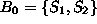was established by the fact that the right-hand-side coefficients of
the constraints in their canonical form with respect to basis
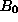are non-negative. We shall address the problem of how to compute an initial bfs
in the more general case where one is not readily available by inspection, in a
later section.
Testing bfs optimality: Checking the sign of the objective function
coefficients for nonbasic variables Notice that the LP objective value
corresponding to basis
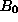is determined by the fact that
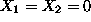, and therefore, z= 0. So, we pose the question: Is it possible that
there exists another bfs with a better objective value? Obviously, any bfs for
which
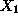and/or
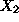is a basic variable has a considerable chance of having a better (i.e., strictly
positive) objective value, since the objective function coefficients for these
variables are positive numbers. Hence, the answer to the previous question is
that the nonnegativity of the objective function coefficients of the
nonbasic variables
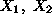implies that there is potential for improvement of the objective value, z,
and both variables
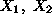are good candidates for entering the basis.
Selecting the entering variable Given that at every
objective-improving iteration the Simplex algorithm considers adjacent
bfs's, it follows that only one of the candidate nonbasic variables will
eventually enter the basis. Typically, the variable selected to enter the basis
is the one that will incur the maximum improvement to the objecive value per
unit of increase of the variable. In our case, this translates to selecting the
(nonbasic) variable with the most positive coefficient in the objective
function, i.e., variable
.
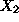Selecting the variable to leave the basis: the ratio test Once we have
selected the variable to enter the basis, we are faced with the question of
which of the current basic variables will be dropped out of it, in order to
obtain the improving adjacent bfs. The logic behind this step is as follows:
Since increasing
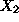from its current (zero) value improves the objective value, we would like to
increase it as much as we can. What constrains us in this increase, is the
requirement to meet the technological constraints:
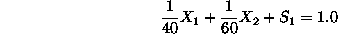
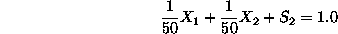
as well as the sign (nonnegativity) restrictions imposed on the LP variables.
In particular, since variable
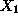will remain nonbasic, its value will remain equal to zero, and therefore it
vanishes from the above set of equations. Hence, we have:
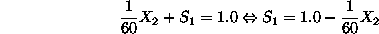
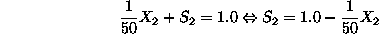
Notice that as
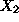increases, both
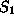and
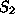are decreased. Obviously,
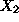cannot increase beyond a value that makes any of
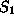and
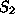negative. So, the maximal allowable increase for
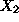is obtained by solving the system of inequalities:
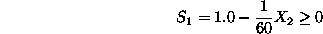
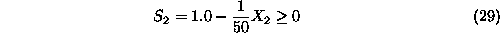
Hence,
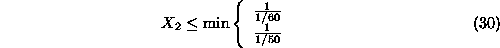
i.e.,
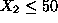. Equation30
is known as the ratio test in the theory of Simplex algorithm, and for
an entering variable
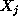, its general form is:
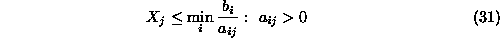
The variable leaving the basis is anyone of those corresponding to a
technological constraint with index i minimizing the ratio of Equation31;
indeed, setting
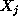to the min-ratio value drives these variables to zero. Hence, in our case, the
variable to leave the basis is
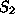, and the new bfs is
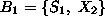. The new (improved) objective value is
.
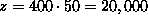Obtaining the canonical form with respect to the new bfs: Pivoting the
entering variable At this point, we must reset to ourselves the question
regarding the optimality of basis
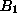. Notice, however, that the way that we addressed this question - as well as all
the other questions - with respect to basis
,
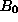was facilitated by the fact that the original set of technological constraints
in Equation28
were in canonical form with respect to that basis. To be able to
address the same set of questions regarding basis
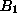, we must transform the original set of constraints into canonical form with
respect to this new basis.
To perform this transformation, first, we rewrite the original LP equations
in the form:
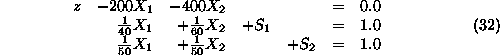
This representation of the LP technological constraints and the
objective-function equation is known as the LP tableau. In particular,
the row corresponding to the objective-function equation is known as the
Row-0 of the tableau, and the coefficients of the (nonbasic) variables in
that row are known as the Row-0 coefficients. Notice also that the
right-hand-side entry of Row-0 provides the objective value of the current bfs.
Under the above tableau representation, the columns corresponding to the
basic variables
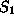and
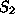are essentially the elementary (unit) vectors:
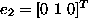and
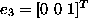, respectively, while the third unit vector
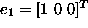is the column of the objective variable z. This is another way to
characterize the fact that the above tableau is in canonical form with respect
to variables
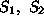. Hence, to obtain the tableau corresponding to basis
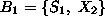, we must convert the column of
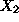in the above tableau to the unit vector
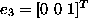, making sure that while we are doing so, we do not alter the content of these
three equations. This can be done by exploiting the following two properties of
a system of linear equations (generally, known as elementary row operations):
- If we multiply any of the system equations with a nonzero
constant, we obtain an equivalent system of equations (i.e., one
with the same solution set).
- if we multiply one of the system equations with a constant and add it to
a second equation, we obtain an equivalent system of equations.
Applying the first of these properties to the third of equations32,
with a coefficient of 50, we get the equivalent system of equations:
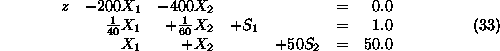
Multiplying the third equation above with -1/60 and adding it to the second
equation, we get:
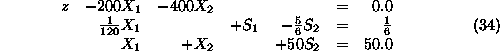
Finally, multiplying the third equation with 400 and adding it to the first
equation, we get:
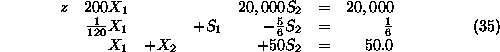
This the new tableau is in canonical form with respect to basis
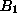. As it was expected, the transformation provided also (automatically) the
values of the new basic variables, and the objective function value
corresponding to the new basis
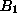(i.e., the right-hand-side of Row-0).
Considering the signs of the Row-0 coefficients in this new tableau, we can
see that increasing any of the non-basic variables from their zero value will
have a descreasing effect on the objective value. Hence, we can conclude that
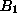is an optimal basis for our example LP. The optimal values for the
basic variables are:
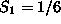and
 ,
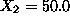and the optimal objective value is
.
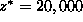You can extend your understanding of this basic Simplex logic, by seeing
how it applies to your own examples. Remember that for this basic Simplex
version to work, all the constraints must be of the "<=" type, and all the
decision variables as well as the rhs-coefficients must be nonnegative.
Submit your examples
Obtaining an initial bfs in the general case As we saw in the previous
example, if all the constraints in the original LP formulation are of the `
'-type, we can readily obtain an initial bfs for Simplex, consisting of all the
slack variables in the corresponding ``standard form'' formulation. In
this section we consider the more general case, where the original LP
formulation might contain also `
'-type inequality as well as equality constraints. To facilitate the subsequent
discussion, let us consider the following LP:
s.t.
which in ``standard form'' becomes:
s.t.
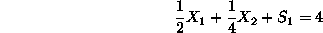
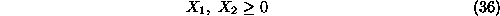
For this LP,
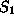can constitute an initial basic variable associated with the first constraint.
However, the excess variable
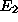cannot be a basic variable for constraint 2, even though it appears only in this
constraint, since this would imply a negative value for it (i.e.,
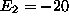), and the resulting basic solution would not be feasible. The last constraint
(#3), does not even involve an auxiliary variable.
To overcome this problem, we ``synthesize'' an initial bfs by introducing
additional (artificial) variables
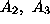for the two ``problematic'' constraints, with
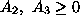. Hence, our initial bfs is
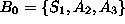, with
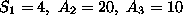. Notice, however, that even though we obtained a bfs for our set of
constraints, we have altered the structure - and therefore, the content - of the
original formulation. In fact, it is easy to check that this bfs (together with
the implied zero values for the nonbasic variables) is not even feasible for the
original LP! On the other hand, if we were able to obtain another bfs for the
modified problem in which the introduced artificial variables are
nonbasic, then this bfs would be also feasible for the original LP: the
artificial variables, being nonbasic, would be equal to zero, and therefore,
they would vanish (i.e., have no effective contribution) in the corresponding
``canonical form'' representation. To obtain the effect just described, we try
to drive the artificial variables to zero, by initially trying to achieve the
following objective:
s.t.
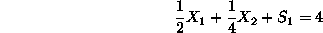
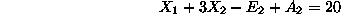
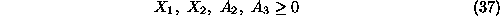
Synthesizing and solving the above LP is known as the Phase I - step
of the Simplex algorithm. If the original LP (Eq.36)
has a feasible solution, then the nonnegativity of
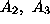implies that the optimal value of this new LP will be zero, and by the
end of its solution we shall also have a feasible bfs for the original
formulation. On the other hand, having a strictly positive optimal objective
value for the LP of Equation37
implies that the artificial variables are absolutely necessary to obtain a
feasible solution for this set of constraints, and therefore, our original LP is
infeasible. Hence, infeasibility is tested during the Phase-I
step of the Simplex algorithm.
Applying the previously described Simplex algorithm on the Phase-I LP of
Equation37,
we obtain the optimal tableau:
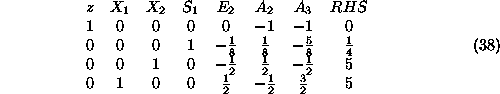
Therefore, a feasible basis for the original LP is
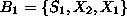. The canonical form of the original tableau with respect to basis
is obtained by:
- dropping the columns corresponding to the artificial variables
from the tableau of Equation38:
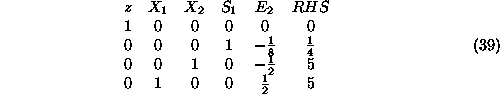
- re-introducing in Row-0 of the resulting tableau the original LP
objective:
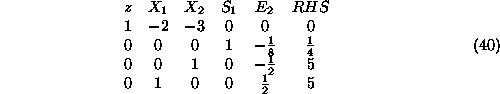
- and, finally, bringing the tableau of Equation40
into canonical form by performing the appropriate elementary row operations
(the Row-0 coefficients of the basic variables
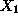and
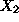must be zero in the corresponding canonical-form formulation):
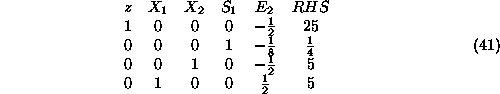
Then, we are ready to restart Simplex, but this time on the original LP
formulation. In this particular case, it is easy to see that, since we have a
minimization problem, the current basis
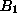is already optimal (i.e., increasing
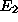from its zero value will only increase the objective function).
Unbounded LP's and LP's with many optimal solutions In the previous
section, we saw that Simplex detects infeasibility while trying to solve the
Phase-I LP. It is instructive to consider how the algorithm behaves on unbounded
LP's as well as on LP's with many optimal solutions. To understand these aspects
of the algorithm, try to implement it on the corresponding examples provided in
Section 2. What is happening?
In your...explorations, and for further experimentation with the (2-phase)
Simplex algorithm, you can use the software developed by Dr. Timothy
Wisniewski, in a collaboration of Argonne National Laboratory and
Northwestern University. In interpreting the program calculations, it should
be noticed, however, that in that code, the reduced costs of the nonbasic
variables are defined as the opposites of the reduced costs used in this
document. Therefore, in the logic of the optimality test, the interpretation of
the reduced cost signs must be inverted. As an example, optimality of a basis
for a minimization problem is implied by the reduced costs of all nonbasic
variables being nonnegative. Additional instructions about the software can be
found in its introductory homepage.
|
