The general LP formulation
Generalizing formulation5,
the general form for a Linear Programming problem is as follows:
Objective Function:
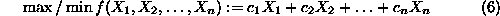
s.t.
Technological Constraints:
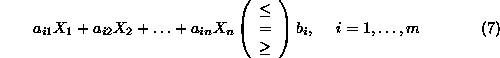
Sign Restrictions:
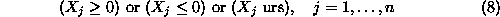
where ``urs'' implies unrestricted in sign.
The formulation of Equations6
to8
has the general structure of a mathematical programming problem, presented in
the introduction of this section, but it is further characterized by the fact
that the functions involved in the problem objective and the left-hand-side of
the technological constraints are linear. It is the assumptions implied
by linearity that to a large extent determine the applicability of the above
model in real-world applications.
To provide a better feeling of the linearity concept, let us assume that the
different decision variables
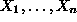correspond to various activities from which any solution will be eventually
synthesized, and the values assigned to the variables by any given solution
indicate the activity level in the considered plan(s). For instance, in the
above example, the two activities are the production of items
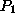and
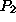, while the activity levels correspond to the daily production volume.
Furthermore, let us assume that each technological constraint of Equation7
imposes some restriction on the consumption of a particular resource. Referring
back to the prototype example, the two problem resources are the daily
production capacity of the two workstations
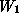and
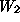. Under this interpretation, the linearity property implies that:
Additivity assumption: - the total consumption of each resource, as well as the overall objective
value are the aggregates of the resource consumptions and the contributions
to the problem objective, resulting by carrying out each activity
independently, and
Proportionality assumption: - these consumptions and contributions for each activity are proportional
to the actual activity level.
It is interesting to notice how the above statement reflects to the logic that
was applied when we derived the technological constraints of the prototype
example: (i) Our assumption that the processing of each unit of product at every
station requires a constant amount of time establishes the proportionality
property for our model. (ii) The assumption that the total processing time
required at every station to meet the production levels of both products is the
aggregate of the processing times required for each product if the corresponding
activity took place independently, implies that our system has an additive
behavior. It is also interesting to see how the linearity assumption restricts
the modeling capabilities of the LP framework: As an example, in the LP
paradigm, we cannot immediately model effects like economies of scale in the
problem cost structure, and/or situations in which resource consumption by one
activity depends on the corresponding consumption by another complementary
activity. In some cases, one can approach these more complicated problems by
applying some linearization scheme. The resulting approximations for
many of these cases have been reported to be quite satisfactory.
Another approximating element in many real-life LP applications results from
the so called divisibility assumption. This assumption refers to the
fact that for LP theory and algortihms to work, the problem variables must be
real. However, in many LP formulations, meaningful values for the
levels of the activities involved can be only integer. This is, for
instance, the case with the production of items
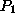and
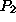in our prototype example. Introducing integrality requirements for some of the
variables in an LP formulation turns the problem to one belonging in the class
of (Mixed) Integer Programming (MIP). The complexity of a MIP problem
is much higher than that of LP's. Actually, the general IP formulation has be
shown to belong to the notorious class of NP-complete problems.
(This is a class of problems that have been ``formally'' shown to be extremely
``hard'' computationally). Given the increased difficulty of solving IP
problems, sometimes in practice, near optimal solutions are obtained by solving
the LP formulation resulting by relaxing the integrality requirements - known as
the LP relaxation of the corresponding IP - and (judiciously) rounding
off the fractional values for the integral variables in the optimal solution.
Such an approach can be more easily justified in cases where the typical values
for the integral variables are in the order of tens or above, since the errors
introduced by the rounding-off are rather small, in a relative sense.
We conclude our discussion on the general LP formulation, by formally
defining the solution search space and optimality. Specifically, we shall define
as the feasible region of the LP of Equations6
to8,
the entire set of vectors
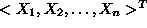that satisfy the technological constraints of Eq.7
and the sign restrictions of Eq.8.
An optimal solution to the problem is any feasible vector that further
satisfies the optimality requirement expressed by Eq.6.
In the next section, we provide a geometric characterization of the feasible
region and the optimality condition, for the special case of LP's having only
two decision variables.
|
