Feasible Regions of Two-Var LP's
The primary idea behind the geometrical representation adopted in the
subsequent analysis, is to correspond every vector
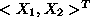denoting the variables of a 2-var LP, to the point with co-ordinates
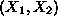in a 2-dim (planar) Cartesian system. Under this correspondence, the
feasible region of a 2-var LP is depicted by the set of points the coordinates
of which satisfy the LP constraints and the sign restrictions. Since all these
constraints are expressed by linear inequalities, to geometrically
characterize the feasible region, we must first characterize the set of points
that constitute the solution space of a linear inequality. Then, the LP
feaslible region will result from the intersection of the solution spaces
corresponding to each technological constraint and/or sign restriction.
|
