Representing the Objective Function in
the LP solution space
The most typical way to represent a two-variable function
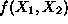is to perceive it as a surface in an (orthogonal) three-dimensional space, where
two of the dimensions correspond to the independent variables
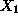and
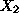, while the third dimension provides the function value for any pair
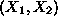. However, in the context of our discussion, we are interested in expressing the
information contained in the two-var LP objective function
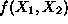
in the Cartesian plane defined by the two independent variables
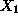and
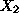. For this purpose, we shall use the concept of contour plots. Contour
plots depict a function by identifying the set of points
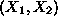that correspond to a constant value of the function
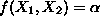, for any given range of
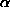's. The plot obtained for any fixed value of
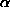is a contour of the function. Studying the structure of a contour is expected to
identify some patterns that essentially depict some useful properties of the
function.
In the case of LP's, the linearity of the objective function implies that any
contour of it will be of the type:
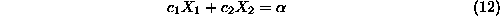
i.e., a straight line. For a maximization (minimization) problem, this line
will be called an isoprofit (isocost) line. Assuming that
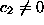(o.w., work with
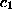), Equation12
can be rewritten as:
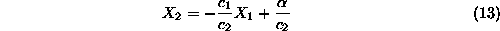
which implies that by changing the value of
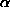, the resulting isoprofit/isocost lines have constant slope and varying
intercept, i.e, they are parallel to each other (which makes sense, since by the
definition of this cocnept, isoprofit/isocost lines cannot intersect). Hence, if
we continously increase
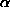from some initial value
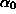, the corresponding isoprofit lines can be obtained by ``sliding'' the isprofit
line corresponding to
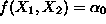parallel to itself, in the direction of increasing or decreasing intercepts,
depending on whether
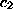is positive or negative.
|
