Graphical solution of the prototype example: a 2-var LP with a unique optimal solution
The `` sliding motion'' described above suggests a way for identifying the
optimal values for, let's say, a max LP problem. The underlying idea is to keep
``sliding'' the isoprofit line
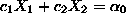in the direction of increasing
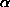's, until we cross the boundary of the LP feasible region. The implementation of
this idea on the prototype LP of Equation5
is depicted in Figure3.
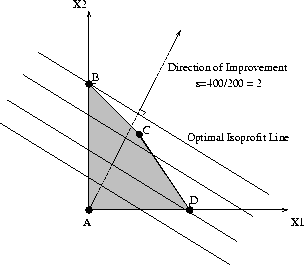
Figure 3: Graphical solution of the prototype example LP
From this figure, it follows that the optimal daily production levels for the
protoype LP are given by the coordinates of the point corresponding to the
intersection of line
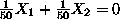with the
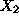-axis, i.e.,
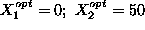. The maximal daily profit is
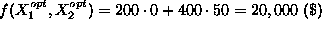. Notice that the optimal point is one of the ``corner'' points of the
feasible region depicted in Figure3.
Can you argue that for the geometry of the feasible region for 2-var LP's
described above, if there is a bounded optimal solution, then there will be one
which corresponds to one of the corner points? (This argument is developed for
the broader context of n-var LP's in the next section.)
|
