| Complex Functions and Linear Mappings |
Example 2.7. Show that the function![[Graphics:Images/ComplexFunLinear_gr_163.gif]](/images/maths/numerical-analysis/calculus/function/ComplexFunLinear_gr_163.gif) maps
the line maps
the line![[Graphics:Images/ComplexFunLinear_gr_164.gif]](/images/maths/numerical-analysis/calculus/function/ComplexFunLinear_gr_164.gif) in
the xy plane onto the line in
the xy plane onto the line![[Graphics:Images/ComplexFunLinear_gr_165.gif]](/images/maths/numerical-analysis/calculus/function/ComplexFunLinear_gr_165.gif) in
the w plane. in
the w plane.
Solution.Method 1:With![[Graphics:Images/ComplexFunLinear_gr_166.gif]](/images/maths/numerical-analysis/calculus/function/ComplexFunLinear_gr_166.gif) ,we
want to describe ,we
want to describe![[Graphics:Images/ComplexFunLinear_gr_167.gif]](/images/maths/numerical-analysis/calculus/function/ComplexFunLinear_gr_167.gif) .We
let .We
let![[Graphics:Images/ComplexFunLinear_gr_168.gif]](/images/maths/numerical-analysis/calculus/function/ComplexFunLinear_gr_168.gif) and
get and
get
![[Graphics:Images/ComplexFunLinear_gr_169.gif]](/images/maths/numerical-analysis/calculus/function/ComplexFunLinear_gr_169.gif)
where
![[Graphics:Images/ComplexFunLinear_gr_170.gif]](/images/maths/numerical-analysis/calculus/function/ComplexFunLinear_gr_170.gif) is the notation for "if and only if."Note what this result says:
is the notation for "if and only if."Note what this result says:![[Graphics:Images/ComplexFunLinear_gr_171.gif]](/images/maths/numerical-analysis/calculus/function/ComplexFunLinear_gr_171.gif) .
The image of A under f,
therefore, is the set .
The image of A under f,
therefore, is the set![[Graphics:Images/ComplexFunLinear_gr_172.gif]](/images/maths/numerical-analysis/calculus/function/ComplexFunLinear_gr_172.gif) . .
Method 2:We write![[Graphics:Images/ComplexFunLinear_gr_173.gif]](/images/maths/numerical-analysis/calculus/function/ComplexFunLinear_gr_173.gif) and
note that the transformation can be given by the equations and
note that the transformation can be given by the equations![[Graphics:Images/ComplexFunLinear_gr_174.gif]](/images/maths/numerical-analysis/calculus/function/ComplexFunLinear_gr_174.gif) .Because
A is described by .Because
A is described by![[Graphics:Images/ComplexFunLinear_gr_175.gif]](/images/maths/numerical-analysis/calculus/function/ComplexFunLinear_gr_175.gif) ,we
can substitute ,we
can substitute![[Graphics:Images/ComplexFunLinear_gr_176.gif]](/images/maths/numerical-analysis/calculus/function/ComplexFunLinear_gr_176.gif) into
the equation into
the equation![[Graphics:Images/ComplexFunLinear_gr_177.gif]](/images/maths/numerical-analysis/calculus/function/ComplexFunLinear_gr_177.gif) to
obtain to
obtain![[Graphics:Images/ComplexFunLinear_gr_178.gif]](/images/maths/numerical-analysis/calculus/function/ComplexFunLinear_gr_178.gif) ,which
we can rewrite as ,which
we can rewrite as![[Graphics:Images/ComplexFunLinear_gr_179.gif]](/images/maths/numerical-analysis/calculus/function/ComplexFunLinear_gr_179.gif) .If
you use this method, be sure to pay careful attention to domains and ranges. .If
you use this method, be sure to pay careful attention to domains and ranges.
We now look at some elementary mappings.If we let![[Graphics:Images/ComplexFunLinear_gr_195.gif]](/images/maths/numerical-analysis/calculus/function/ComplexFunLinear_gr_195.gif) denote
a fixed complex constant, the transformation denote
a fixed complex constant, the transformation
![[Graphics:Images/ComplexFunLinear_gr_196.gif]](/images/maths/numerical-analysis/calculus/function/ComplexFunLinear_gr_196.gif)
is a one-to-one mapping of the z-plane onto the w-plane and is called a
translation.This transformation can be visualized as a rigid
translation whereby the pointzis displaced through the vector![[Graphics:Images/ComplexFunLinear_gr_197.gif]](/images/maths/numerical-analysis/calculus/function/ComplexFunLinear_gr_197.gif) to
its new position to
its new position![[Graphics:Images/ComplexFunLinear_gr_198.gif]](/images/maths/numerical-analysis/calculus/function/ComplexFunLinear_gr_198.gif) .The
inverse mapping is given by .The
inverse mapping is given by
![[Graphics:Images/ComplexFunLinear_gr_199.gif]](/images/maths/numerical-analysis/calculus/function/ComplexFunLinear_gr_199.gif)
and shows thatTis a one-to-one mapping from the z-plane onto the w-plane.
The effect of a translation is depicted in Figure 2.5.
![[Graphics:Images/ComplexFunLinear_gr_200.gif]](/images/maths/numerical-analysis/calculus/function/ComplexFunLinear_gr_200.gif)
Figure 2.5The
translation![[Graphics:Images/ComplexFunLinear_gr_201.gif]](/images/maths/numerical-analysis/calculus/function/ComplexFunLinear_gr_201.gif) . .
If we let![[Graphics:Images/ComplexFunLinear_gr_202.gif]](/images/maths/numerical-analysis/calculus/function/ComplexFunLinear_gr_202.gif) be
a fixed real number, then for be
a fixed real number, then for![[Graphics:Images/ComplexFunLinear_gr_203.gif]](/images/maths/numerical-analysis/calculus/function/ComplexFunLinear_gr_203.gif) ,the
transformation ,the
transformation
![[Graphics:Images/ComplexFunLinear_gr_204.gif]](/images/maths/numerical-analysis/calculus/function/ComplexFunLinear_gr_204.gif)
is a one-to-one mapping of the z-plane onto the w-plane and is called a
rotation.It can be visualized as a rigid rotation whereby the
pointzis rotated about the origin through an angle![[Graphics:Images/ComplexFunLinear_gr_205.gif]](/images/maths/numerical-analysis/calculus/function/ComplexFunLinear_gr_205.gif) to
its new position to
its new position![[Graphics:Images/ComplexFunLinear_gr_206.gif]](/images/maths/numerical-analysis/calculus/function/ComplexFunLinear_gr_206.gif) .If
we use polar coordinates and designate .If
we use polar coordinates and designate![[Graphics:Images/ComplexFunLinear_gr_207.gif]](/images/maths/numerical-analysis/calculus/function/ComplexFunLinear_gr_207.gif) in
the w-plane, then the inverse mapping is in
the w-plane, then the inverse mapping is
![[Graphics:Images/ComplexFunLinear_gr_208.gif]](/images/maths/numerical-analysis/calculus/function/ComplexFunLinear_gr_208.gif) . .
This analysis shows thatRis a one-to-one mapping from the z-plane onto the
w-plane.The effect of rotation is depicted in Figure 2.6.
![[Graphics:Images/ComplexFunLinear_gr_209.gif]](/images/maths/numerical-analysis/calculus/function/ComplexFunLinear_gr_209.gif)
Figure 2.6The
rotation![[Graphics:Images/ComplexFunLinear_gr_210.gif]](/images/maths/numerical-analysis/calculus/function/ComplexFunLinear_gr_210.gif) . .
Example 2.8.The ellipse centered at the
origin with a horizontal major axis of 4 units and vertical minor axis of 2
units can be represented by the parametric equation
![[Graphics:Images/ComplexFunLinear_gr_211.gif]](/images/maths/numerical-analysis/calculus/function/ComplexFunLinear_gr_211.gif) ,for ,for![[Graphics:Images/ComplexFunLinear_gr_212.gif]](/images/maths/numerical-analysis/calculus/function/ComplexFunLinear_gr_212.gif) . .
Suppose we wanted to rotate the ellipse by an angle of
![[Graphics:Images/ComplexFunLinear_gr_213.gif]](/images/maths/numerical-analysis/calculus/function/ComplexFunLinear_gr_213.gif) radians and shift the center of the ellipse 2 units to the right and 1 unit up.
Using complex arithmetic, we can easily generate a parametric equation
r(t) that does so:
radians and shift the center of the ellipse 2 units to the right and 1 unit up.
Using complex arithmetic, we can easily generate a parametric equation
r(t) that does so:
![[Graphics:Images/ComplexFunLinear_gr_214.gif]](/images/maths/numerical-analysis/calculus/function/ComplexFunLinear_gr_214.gif)
for![[Graphics:Images/ComplexFunLinear_gr_215.gif]](/images/maths/numerical-analysis/calculus/function/ComplexFunLinear_gr_215.gif) .Figure
2.7 shows parametric plots of these ellipses. .Figure
2.7 shows parametric plots of these ellipses.
![[Graphics:Images/ComplexFunLinear_gr_216.gif]](/images/maths/numerical-analysis/calculus/function/ComplexFunLinear_gr_216.gif)
Figure 2.7(a)Plot of the
original ellipse(b)Plot
of the rotated ellipse
![[Graphics:Images/ComplexFunLinear_gr_217.gif]](/images/maths/numerical-analysis/calculus/function/ComplexFunLinear_gr_217.gif) ![[Graphics:Images/ComplexFunLinear_gr_218.gif]](/images/maths/numerical-analysis/calculus/function/ComplexFunLinear_gr_218.gif)
If we let![[Graphics:Images/ComplexFunLinear_gr_224.gif]](/images/maths/numerical-analysis/calculus/function/ComplexFunLinear_gr_224.gif) be
a fixed positive real number, then the transformation be
a fixed positive real number, then the transformation
![[Graphics:Images/ComplexFunLinear_gr_225.gif]](/images/maths/numerical-analysis/calculus/function/ComplexFunLinear_gr_225.gif)
is a one-to-one mapping of the z-plane onto the w-plane and is called a
magnification.If![[Graphics:Images/ComplexFunLinear_gr_226.gif]](/images/maths/numerical-analysis/calculus/function/ComplexFunLinear_gr_226.gif) ,it
has the effect of stretching the distance between points by the
factorK.If ,it
has the effect of stretching the distance between points by the
factorK.If![[Graphics:Images/ComplexFunLinear_gr_227.gif]](/images/maths/numerical-analysis/calculus/function/ComplexFunLinear_gr_227.gif) ,then
it reduces the distance between points by the factorK.The inverse
transformation is given by ,then
it reduces the distance between points by the factorK.The inverse
transformation is given by
![[Graphics:Images/ComplexFunLinear_gr_228.gif]](/images/maths/numerical-analysis/calculus/function/ComplexFunLinear_gr_228.gif)
and shows thatSis a one-to-one mapping from the z-plane onto the
w-plane.The effect of magnification is shown in Figure 2.8.
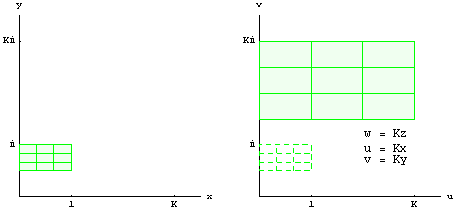
Figure 2.8The
magnification![[Graphics:Images/ComplexFunLinear_gr_229.gif]](/images/maths/numerical-analysis/calculus/function/ComplexFunLinear_gr_229.gif) . .
Finally, if we let![[Graphics:Images/ComplexFunLinear_gr_230.gif]](/images/maths/numerical-analysis/calculus/function/ComplexFunLinear_gr_230.gif) and and![[Graphics:Images/ComplexFunLinear_gr_231.gif]](/images/maths/numerical-analysis/calculus/function/ComplexFunLinear_gr_231.gif) ,
where ,
where![[Graphics:Images/ComplexFunLinear_gr_232.gif]](/images/maths/numerical-analysis/calculus/function/ComplexFunLinear_gr_232.gif) is
a positive real number, then the transformation is
a positive real number, then the transformation
![[Graphics:Images/ComplexFunLinear_gr_233.gif]](/images/maths/numerical-analysis/calculus/function/ComplexFunLinear_gr_233.gif)
is a one-to-one mapping of the z-plane onto the
w-plane and is called a
linear transformation.It can be considered as the composition of a
rotation, a magnification, and a translation.It has the effect of rotating the
plane though an angle given by![[Graphics:Images/ComplexFunLinear_gr_234.gif]](/images/maths/numerical-analysis/calculus/function/ComplexFunLinear_gr_234.gif) ,followed
by a magnification by the factor ,followed
by a magnification by the factor![[Graphics:Images/ComplexFunLinear_gr_235.gif]](/images/maths/numerical-analysis/calculus/function/ComplexFunLinear_gr_235.gif) ,
followed by a translation by the vector ,
followed by a translation by the vector![[Graphics:Images/ComplexFunLinear_gr_236.gif]](/images/maths/numerical-analysis/calculus/function/ComplexFunLinear_gr_236.gif) .The
inverse mapping is given by .The
inverse mapping is given by![[Graphics:Images/ComplexFunLinear_gr_237.gif]](/images/maths/numerical-analysis/calculus/function/ComplexFunLinear_gr_237.gif) and
shows that L is a one-to-one mapping from the
z-plane onto the w-plane. and
shows that L is a one-to-one mapping from the
z-plane onto the w-plane.
Example 2.9.Show that the linear
transformation![[Graphics:Images/ComplexFunLinear_gr_238.gif]](/images/maths/numerical-analysis/calculus/function/ComplexFunLinear_gr_238.gif) maps
the right half plane maps
the right half plane![[Graphics:Images/ComplexFunLinear_gr_239.gif]](/images/maths/numerical-analysis/calculus/function/ComplexFunLinear_gr_239.gif) onto
the upper half plane onto
the upper half plane![[Graphics:Images/ComplexFunLinear_gr_240.gif]](/images/maths/numerical-analysis/calculus/function/ComplexFunLinear_gr_240.gif) . .
Solution.Method 1:Let![[Graphics:Images/ComplexFunLinear_gr_241.gif]](/images/maths/numerical-analysis/calculus/function/ComplexFunLinear_gr_241.gif) .To
describe .To
describe![[Graphics:Images/ComplexFunLinear_gr_242.gif]](/images/maths/numerical-analysis/calculus/function/ComplexFunLinear_gr_242.gif) ,we
solve ,we
solve![[Graphics:Images/ComplexFunLinear_gr_243.gif]](/images/maths/numerical-analysis/calculus/function/ComplexFunLinear_gr_243.gif) for
z to get for
z to get![[Graphics:Images/ComplexFunLinear_gr_244.gif]](/images/maths/numerical-analysis/calculus/function/ComplexFunLinear_gr_244.gif) .We
have the following .We
have the following
![[Graphics:Images/ComplexFunLinear_gr_245.gif]](/images/maths/numerical-analysis/calculus/function/ComplexFunLinear_gr_245.gif)
Thus![[Graphics:Images/ComplexFunLinear_gr_246.gif]](/images/maths/numerical-analysis/calculus/function/ComplexFunLinear_gr_246.gif) ,which
is the same as saying ,which
is the same as saying![[Graphics:Images/ComplexFunLinear_gr_247.gif]](/images/maths/numerical-analysis/calculus/function/ComplexFunLinear_gr_247.gif) . .
Method 2: When we write![[Graphics:Images/ComplexFunLinear_gr_248.gif]](/images/maths/numerical-analysis/calculus/function/ComplexFunLinear_gr_248.gif) in
Cartesian form as in
Cartesian form as
![[Graphics:Images/ComplexFunLinear_gr_249.gif]](/images/maths/numerical-analysis/calculus/function/ComplexFunLinear_gr_249.gif) , ,
we see that the transformation can be given by the equations![[Graphics:Images/ComplexFunLinear_gr_250.gif]](/images/maths/numerical-analysis/calculus/function/ComplexFunLinear_gr_250.gif) and
and
![[Graphics:Images/ComplexFunLinear_gr_251.gif]](/images/maths/numerical-analysis/calculus/function/ComplexFunLinear_gr_251.gif) .Substituting .Substituting![[Graphics:Images/ComplexFunLinear_gr_252.gif]](/images/maths/numerical-analysis/calculus/function/ComplexFunLinear_gr_252.gif) in
the inequality in
the inequality![[Graphics:Images/ComplexFunLinear_gr_253.gif]](/images/maths/numerical-analysis/calculus/function/ComplexFunLinear_gr_253.gif) gives gives![[Graphics:Images/ComplexFunLinear_gr_254.gif]](/images/maths/numerical-analysis/calculus/function/ComplexFunLinear_gr_254.gif) ,or ,or![[Graphics:Images/ComplexFunLinear_gr_255.gif]](/images/maths/numerical-analysis/calculus/function/ComplexFunLinear_gr_255.gif) ,which
is the upper half-plane ,which
is the upper half-plane![[Graphics:Images/ComplexFunLinear_gr_256.gif]](/images/maths/numerical-analysis/calculus/function/ComplexFunLinear_gr_256.gif) . .
Method 3:The effect of the transformation![[Graphics:Images/ComplexFunLinear_gr_257.gif]](/images/maths/numerical-analysis/calculus/function/ComplexFunLinear_gr_257.gif) is a rotation of the plane through the angle
is a rotation of the plane through the angle![[Graphics:Images/ComplexFunLinear_gr_258.gif]](/images/maths/numerical-analysis/calculus/function/ComplexFunLinear_gr_258.gif) (when z is multiplied by
(when z is multiplied by
![[Graphics:Images/ComplexFunLinear_gr_259.gif]](/images/maths/numerical-analysis/calculus/function/ComplexFunLinear_gr_259.gif) )
followed by a translation by the vector )
followed by a translation by the vector![[Graphics:Images/ComplexFunLinear_gr_260.gif]](/images/maths/numerical-analysis/calculus/function/ComplexFunLinear_gr_260.gif) .The
first operation yields the set .The
first operation yields the set![[Graphics:Images/ComplexFunLinear_gr_261.gif]](/images/maths/numerical-analysis/calculus/function/ComplexFunLinear_gr_261.gif) .The
second shifts this set up 1 unit, resulting in
the set .The
second shifts this set up 1 unit, resulting in
the set![[Graphics:Images/ComplexFunLinear_gr_262.gif]](/images/maths/numerical-analysis/calculus/function/ComplexFunLinear_gr_262.gif) .We
illustrate this result in Figure 2.9. .We
illustrate this result in Figure 2.9.
![[Graphics:Images/ComplexFunLinear_gr_263.gif]](/images/maths/numerical-analysis/calculus/function/ComplexFunLinear_gr_263.gif)
Figure 2.9The linear
transformation![[Graphics:Images/ComplexFunLinear_gr_264.gif]](/images/maths/numerical-analysis/calculus/function/ComplexFunLinear_gr_264.gif) . .
Translations and rotations preserve angles.First, magnifications
rescale distance by a factor K, so it follows that triangles are mapped onto
similar triangles, preserving angles.Then, because a linear transformation can
be considered to be a composition of a rotation, a magnification, and a
translation, it follows that linear transformations preserve
angles.Consequently, any geometric object is mapped onto an object that is
similar to the original object; hence linear transformations can be called
similarity mappings.
Note. The usage of the phrase "linear
transformation" in a "complex analysis course" is different than that the
usage in "linear algebra courses".
Example 2.10.Show that the image of the
open disk![[Graphics:Images/ComplexFunLinear_gr_282.gif]](/images/maths/numerical-analysis/calculus/function/ComplexFunLinear_gr_282.gif) under
the linear transformation under
the linear transformation![[Graphics:Images/ComplexFunLinear_gr_283.gif]](/images/maths/numerical-analysis/calculus/function/ComplexFunLinear_gr_283.gif) is
the open disk is
the open disk![[Graphics:Images/ComplexFunLinear_gr_284.gif]](/images/maths/numerical-analysis/calculus/function/ComplexFunLinear_gr_284.gif) . .
Solution.The inverse transformation is![[Graphics:Images/ComplexFunLinear_gr_285.gif]](/images/maths/numerical-analysis/calculus/function/ComplexFunLinear_gr_285.gif) ,so
if we designate the range of f as
B, then ,so
if we designate the range of f as
B, then
![[Graphics:Images/ComplexFunLinear_gr_286.gif]](/images/maths/numerical-analysis/calculus/function/ComplexFunLinear_gr_286.gif)
![[Graphics:Images/ComplexFunLinear_gr_287.gif]](/images/maths/numerical-analysis/calculus/function/ComplexFunLinear_gr_287.gif) ![[Graphics:Images/ComplexFunLinear_gr_288.gif]](/images/maths/numerical-analysis/calculus/function/ComplexFunLinear_gr_288.gif)
![[Graphics:Images/ComplexFunLinear_gr_289.gif]](/images/maths/numerical-analysis/calculus/function/ComplexFunLinear_gr_289.gif)
Hence the disk with center![[Graphics:Images/ComplexFunLinear_gr_290.gif]](/images/maths/numerical-analysis/calculus/function/ComplexFunLinear_gr_290.gif) and
radius 1 is mapped one-to-one and onto the disk
with center and
radius 1 is mapped one-to-one and onto the disk
with center![[Graphics:Images/ComplexFunLinear_gr_291.gif]](/images/maths/numerical-analysis/calculus/function/ComplexFunLinear_gr_291.gif) and
radius 5 as shown in Figure 2.10. and
radius 5 as shown in Figure 2.10.
![[Graphics:Images/ComplexFunLinear_gr_292.gif]](/images/maths/numerical-analysis/calculus/function/ComplexFunLinear_gr_292.gif)
Figure
2.10The
mapping![[Graphics:Images/ComplexFunLinear_gr_293.gif]](/images/maths/numerical-analysis/calculus/function/ComplexFunLinear_gr_293.gif) . .
Example 2.11.Show that the image of the
right half plane![[Graphics:Images/ComplexFunLinear_gr_312.gif]](/images/maths/numerical-analysis/calculus/function/ComplexFunLinear_gr_312.gif) under
the linear transformation under
the linear transformation![[Graphics:Images/ComplexFunLinear_gr_313.gif]](/images/maths/numerical-analysis/calculus/function/ComplexFunLinear_gr_313.gif) is
the half plane is
the half plane![[Graphics:Images/ComplexFunLinear_gr_314.gif]](/images/maths/numerical-analysis/calculus/function/ComplexFunLinear_gr_314.gif) . .
Solution.The inverse transformation is given by
![[Graphics:Images/ComplexFunLinear_gr_315.gif]](/images/maths/numerical-analysis/calculus/function/ComplexFunLinear_gr_315.gif) , ,
which we write as
![[Graphics:Images/ComplexFunLinear_gr_316.gif]](/images/maths/numerical-analysis/calculus/function/ComplexFunLinear_gr_316.gif) . .
Substituting![[Graphics:Images/ComplexFunLinear_gr_317.gif]](/images/maths/numerical-analysis/calculus/function/ComplexFunLinear_gr_317.gif) intoe intoe![[Graphics:Images/ComplexFunLinear_gr_318.gif]](/images/maths/numerical-analysis/calculus/function/ComplexFunLinear_gr_318.gif) gives gives![[Graphics:Images/ComplexFunLinear_gr_319.gif]](/images/maths/numerical-analysis/calculus/function/ComplexFunLinear_gr_319.gif) ,which
simplifies ,which
simplifies![[Graphics:Images/ComplexFunLinear_gr_320.gif]](/images/maths/numerical-analysis/calculus/function/ComplexFunLinear_gr_320.gif) .Figure
2.11 illustrates the mapping. .Figure
2.11 illustrates the mapping.
![[Graphics:Images/ComplexFunLinear_gr_321.gif]](/images/maths/numerical-analysis/calculus/function/ComplexFunLinear_gr_321.gif)
Figure
2.11The the
linear transformation![[Graphics:Images/ComplexFunLinear_gr_322.gif]](/images/maths/numerical-analysis/calculus/function/ComplexFunLinear_gr_322.gif) . .
|

