The Accelerated and Modified Newton Methods
Background
Newton's method is commonly used to find the
root of an equation.If the root is simple then the extension to Halley's
method will increase the order of convergence from quadratic to cubic.At a
multiple root it can be speed up with the accelerated Newton-Raphson and
modified Newton-Raphson methods.
Theorem (Newton-Raphson Theorem ).Assume that
![[Graphics:Images/NewtonAccelerateMod_gr_1.gif]](/images/maths/numerical-analysis/nonlinear/accelerate/NewtonAccelerateMod_gr_1.gif) and there exists a number
and there exists a number
![[Graphics:Images/NewtonAccelerateMod_gr_2.gif]](/images/maths/numerical-analysis/nonlinear/accelerate/NewtonAccelerateMod_gr_2.gif) ,
where ,
where
![[Graphics:Images/NewtonAccelerateMod_gr_3.gif]](/images/maths/numerical-analysis/nonlinear/accelerate/NewtonAccelerateMod_gr_3.gif) .If .If![[Graphics:Images/NewtonAccelerateMod_gr_4.gif]](/images/maths/numerical-analysis/nonlinear/accelerate/NewtonAccelerateMod_gr_4.gif) ,
then there exists a ,
then there exists a
![[Graphics:Images/NewtonAccelerateMod_gr_5.gif]](/images/maths/numerical-analysis/nonlinear/accelerate/NewtonAccelerateMod_gr_5.gif) such that the sequence
such that the sequence
![[Graphics:Images/NewtonAccelerateMod_gr_6.gif]](/images/maths/numerical-analysis/nonlinear/accelerate/NewtonAccelerateMod_gr_6.gif) defined by the iteration
defined by the iteration
![[Graphics:Images/NewtonAccelerateMod_gr_7.gif]](/images/maths/numerical-analysis/nonlinear/accelerate/NewtonAccelerateMod_gr_7.gif) for for![[Graphics:Images/NewtonAccelerateMod_gr_8.gif]](/images/maths/numerical-analysis/nonlinear/accelerate/NewtonAccelerateMod_gr_8.gif)
will converge to
![[Graphics:Images/NewtonAccelerateMod_gr_9.gif]](/images/maths/numerical-analysis/nonlinear/accelerate/NewtonAccelerateMod_gr_9.gif) for any initial approximation
for any initial approximation![[Graphics:Images/NewtonAccelerateMod_gr_10.gif]](/images/maths/numerical-analysis/nonlinear/accelerate/NewtonAccelerateMod_gr_10.gif) . .
Definition (Order of a Root)Assume
thatf(x)and its derivatives![[Graphics:Images/NewtonAccelerateMod_gr_11.gif]](/images/maths/numerical-analysis/nonlinear/accelerate/NewtonAccelerateMod_gr_11.gif) are
defined and continuous on an interval aboutx = p.We say thatf(x) = 0has
a root of ordermatx = pif and only
if are
defined and continuous on an interval aboutx = p.We say thatf(x) = 0has
a root of ordermatx = pif and only
if
![[Graphics:Images/NewtonAccelerateMod_gr_12.gif]](/images/maths/numerical-analysis/nonlinear/accelerate/NewtonAccelerateMod_gr_12.gif) . .
A root of orderm
= 1is often called a
simple root, and ifm
> 1it is called a
multiple root.A root of orderm
= 2is sometimes called a
double root, and so on.The next
result will illuminate these concepts.
Definition (Order of
Convergence)Assume that![[Graphics:Images/NewtonAccelerateMod_gr_13.gif]](/images/maths/numerical-analysis/nonlinear/accelerate/NewtonAccelerateMod_gr_13.gif) converges top,and set
converges top,and set![[Graphics:Images/NewtonAccelerateMod_gr_14.gif]](/images/maths/numerical-analysis/nonlinear/accelerate/NewtonAccelerateMod_gr_14.gif) .If
two positive constants .If
two positive constants![[Graphics:Images/NewtonAccelerateMod_gr_15.gif]](/images/maths/numerical-analysis/nonlinear/accelerate/NewtonAccelerateMod_gr_15.gif) exist,
and exist,
and
![[Graphics:Images/NewtonAccelerateMod_gr_16.gif]](/images/maths/numerical-analysis/nonlinear/accelerate/NewtonAccelerateMod_gr_16.gif)
then the sequence is said to converge topwith
order of convergence R.The
numberAis called the
asymptotic error constant.The cases![[Graphics:Images/NewtonAccelerateMod_gr_17.gif]](/images/maths/numerical-analysis/nonlinear/accelerate/NewtonAccelerateMod_gr_17.gif) are
given specialconsideration. are
given specialconsideration.
(i)If![[Graphics:Images/NewtonAccelerateMod_gr_18.gif]](/images/maths/numerical-analysis/nonlinear/accelerate/NewtonAccelerateMod_gr_18.gif) ,
the convergence of ,
the convergence of![[Graphics:Images/NewtonAccelerateMod_gr_19.gif]](/images/maths/numerical-analysis/nonlinear/accelerate/NewtonAccelerateMod_gr_19.gif) is
called linear. is
called linear.
(ii)If![[Graphics:Images/NewtonAccelerateMod_gr_20.gif]](/images/maths/numerical-analysis/nonlinear/accelerate/NewtonAccelerateMod_gr_20.gif) ,
the convergence of ,
the convergence of![[Graphics:Images/NewtonAccelerateMod_gr_21.gif]](/images/maths/numerical-analysis/nonlinear/accelerate/NewtonAccelerateMod_gr_21.gif) is
called quadratic. is
called quadratic.
Theorem (Convergence Rate for
Newton-Raphson Iteration)Assume that
Newton-Raphson iteration produces a sequence![[Graphics:Images/NewtonAccelerateMod_gr_22.gif]](/images/maths/numerical-analysis/nonlinear/accelerate/NewtonAccelerateMod_gr_22.gif) that converges to the rootpof the function
that converges to the rootpof the function![[Graphics:Images/NewtonAccelerateMod_gr_23.gif]](/images/maths/numerical-analysis/nonlinear/accelerate/NewtonAccelerateMod_gr_23.gif) . .
Ifpis a simple root, then convergence is
quadratic and![[Graphics:Images/NewtonAccelerateMod_gr_24.gif]](/images/maths/numerical-analysis/nonlinear/accelerate/NewtonAccelerateMod_gr_24.gif) forksufficiently
large. forksufficiently
large.
Ifpis a multiple root of orderm,then
convergence is linear and![[Graphics:Images/NewtonAccelerateMod_gr_25.gif]](/images/maths/numerical-analysis/nonlinear/accelerate/NewtonAccelerateMod_gr_25.gif) forksufficiently
large. forksufficiently
large.
Algorithm (Newton-Raphson Iteration).To
find a root of![[Graphics:Images/NewtonAccelerateMod_gr_26.gif]](/images/maths/numerical-analysis/nonlinear/accelerate/NewtonAccelerateMod_gr_26.gif) given
an initial approximation given
an initial approximation![[Graphics:Images/NewtonAccelerateMod_gr_27.gif]](/images/maths/numerical-analysis/nonlinear/accelerate/NewtonAccelerateMod_gr_27.gif) using
the iteration using
the iteration
![[Graphics:Images/NewtonAccelerateMod_gr_28.gif]](/images/maths/numerical-analysis/nonlinear/accelerate/NewtonAccelerateMod_gr_28.gif) for for![[Graphics:Images/NewtonAccelerateMod_gr_29.gif]](/images/maths/numerical-analysis/nonlinear/accelerate/NewtonAccelerateMod_gr_29.gif) . .
Mathematica Subroutine (Newton-Raphson Iteration).
![[Graphics:Images/NewtonAccelerateMod_gr_30.gif]](/images/maths/numerical-analysis/nonlinear/accelerate/NewtonAccelerateMod_gr_30.gif)
Theorem (Acceleration of
Newton-Raphson Iteration)Given that
the Newton-Raphson algorithm produces a sequence that converges linearly to the
root![[Graphics:Images/NewtonAccelerateMod_gr_112.gif]](/images/maths/numerical-analysis/nonlinear/accelerate/NewtonAccelerateMod_gr_112.gif) of
order of
order![[Graphics:Images/NewtonAccelerateMod_gr_113.gif]](/images/maths/numerical-analysis/nonlinear/accelerate/NewtonAccelerateMod_gr_113.gif) .Then
the accelerated Newton-Raphson formula .Then
the accelerated Newton-Raphson formula
![[Graphics:Images/NewtonAccelerateMod_gr_114.gif]](/images/maths/numerical-analysis/nonlinear/accelerate/NewtonAccelerateMod_gr_114.gif) for for![[Graphics:Images/NewtonAccelerateMod_gr_115.gif]](/images/maths/numerical-analysis/nonlinear/accelerate/NewtonAccelerateMod_gr_115.gif)
will produce a sequence
![[Graphics:Images/NewtonAccelerateMod_gr_116.gif]](/images/maths/numerical-analysis/nonlinear/accelerate/NewtonAccelerateMod_gr_116.gif) that converges quadratically top.
that converges quadratically top.
Mathematica Subroutine (Accelerated Newton-Raphson
Iteration).
![[Graphics:Images/NewtonAccelerateMod_gr_117.gif]](/images/maths/numerical-analysis/nonlinear/accelerate/NewtonAccelerateMod_gr_117.gif)
Example.Use the accelerated Newton's
method to find the double root![[Graphics:Images/NewtonAccelerateMod_gr_118.gif]](/images/maths/numerical-analysis/nonlinear/accelerate/NewtonAccelerateMod_gr_118.gif) ,of
the cubic polynomial ,of
the cubic polynomial![[Graphics:Images/NewtonAccelerateMod_gr_119.gif]](/images/maths/numerical-analysis/nonlinear/accelerate/NewtonAccelerateMod_gr_119.gif) .Use
the starting value .Use
the starting value![[Graphics:Images/NewtonAccelerateMod_gr_120.gif]](/images/maths/numerical-analysis/nonlinear/accelerate/NewtonAccelerateMod_gr_120.gif)
Solution.
More Background
Iff(x)has
a root of multiplicitymatx=p,
thenf(x)can
be exssed in the form
![[Graphics:Images/NewtonAccelerateMod_gr_223.gif]](/images/maths/numerical-analysis/nonlinear/accelerate/NewtonAccelerateMod_gr_223.gif)
where![[Graphics:Images/NewtonAccelerateMod_gr_224.gif]](/images/maths/numerical-analysis/nonlinear/accelerate/NewtonAccelerateMod_gr_224.gif) .In
this situation, the functionh(x)is defined
by .In
this situation, the functionh(x)is defined
by
![[Graphics:Images/NewtonAccelerateMod_gr_225.gif]](/images/maths/numerical-analysis/nonlinear/accelerate/NewtonAccelerateMod_gr_225.gif)
and it is easy to prove thath(x)has
a simple root atx=p.When
Newton's method is applied for finding the rootx=pofh(x)we
obtain the following result.
Theorem (Modified
Newton-Raphson Iteration)Given that
the Newton-Raphson algorithm produces a sequence that converges linearly to the
root![[Graphics:Images/NewtonAccelerateMod_gr_226.gif]](/images/maths/numerical-analysis/nonlinear/accelerate/NewtonAccelerateMod_gr_226.gif) of
multiplicity of
multiplicity![[Graphics:Images/NewtonAccelerateMod_gr_227.gif]](/images/maths/numerical-analysis/nonlinear/accelerate/NewtonAccelerateMod_gr_227.gif) .Then
the modified Newton-Raphson formula .Then
the modified Newton-Raphson formula
![[Graphics:Images/NewtonAccelerateMod_gr_228.gif]](/images/maths/numerical-analysis/nonlinear/accelerate/NewtonAccelerateMod_gr_228.gif)
which can be simplified as
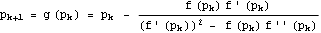 for for![[Graphics:Images/NewtonAccelerateMod_gr_230.gif]](/images/maths/numerical-analysis/nonlinear/accelerate/NewtonAccelerateMod_gr_230.gif)
will produce a sequence
![[Graphics:Images/NewtonAccelerateMod_gr_231.gif]](/images/maths/numerical-analysis/nonlinear/accelerate/NewtonAccelerateMod_gr_231.gif) that converges quadratically top.
that converges quadratically top.
Mathematica Subroutine (Modified Newton-Raphson
Iteration).
![[Graphics:Images/NewtonAccelerateMod_gr_232.gif]](/images/maths/numerical-analysis/nonlinear/accelerate/NewtonAccelerateMod_gr_232.gif)
|