Fixed Point Iteration and Newton's Method in 2D and 3D
Background
Iterative techniques will now be introduced that extend the fixed point and
Newton methods for finding a root of an equation.We desire to have a method
for finding a solution for the system of nonlinear equations
![[Graphics:Images/NewtonSystemMod_gr_1.gif]](/images/maths/numerical-analysis/nonlinear/fixed-iterate/NewtonSystemMod_gr_1.gif)
(1)
![[Graphics:Images/NewtonSystemMod_gr_2.gif]](/images/maths/numerical-analysis/nonlinear/fixed-iterate/NewtonSystemMod_gr_2.gif) . .
Each equation in (1) implicitly defines a curve in the plane and we want to find
their points of intersection.Our first method will be be fixed point iteration
and the second one will be Newton's method.
Definition (Jacobian Matrix).Assume
that
![[Graphics:Images/NewtonSystemMod_gr_3.gif]](/images/maths/numerical-analysis/nonlinear/fixed-iterate/NewtonSystemMod_gr_3.gif) are functions of the independent variables
are functions of the independent variables
![[Graphics:Images/NewtonSystemMod_gr_4.gif]](/images/maths/numerical-analysis/nonlinear/fixed-iterate/NewtonSystemMod_gr_4.gif) ,
then their
Jacobian matrix ,
then their
Jacobian matrix![[Graphics:Images/NewtonSystemMod_gr_5.gif]](/images/maths/numerical-analysis/nonlinear/fixed-iterate/NewtonSystemMod_gr_5.gif) is
is
![[Graphics:Images/NewtonSystemMod_gr_6.gif]](/images/maths/numerical-analysis/nonlinear/fixed-iterate/NewtonSystemMod_gr_6.gif) . .
Similarly, if![[Graphics:Images/NewtonSystemMod_gr_7.gif]](/images/maths/numerical-analysis/nonlinear/fixed-iterate/NewtonSystemMod_gr_7.gif) are functions of the independent variables
are functions of the independent variables![[Graphics:Images/NewtonSystemMod_gr_8.gif]](/images/maths/numerical-analysis/nonlinear/fixed-iterate/NewtonSystemMod_gr_8.gif) ,
then their
Jacobian matrix ,
then their
Jacobian matrix![[Graphics:Images/NewtonSystemMod_gr_9.gif]](/images/maths/numerical-analysis/nonlinear/fixed-iterate/NewtonSystemMod_gr_9.gif) is
is
![[Graphics:Images/NewtonSystemMod_gr_10.gif]](/images/maths/numerical-analysis/nonlinear/fixed-iterate/NewtonSystemMod_gr_10.gif) . .
Generalized Differential
For a function of several variables, the differential is used to show how
changes of the independent variables affect the change in the dependent
variables. Suppose that we have
![[Graphics:Images/NewtonSystemMod_gr_11.gif]](/images/maths/numerical-analysis/nonlinear/fixed-iterate/NewtonSystemMod_gr_11.gif)
![[Graphics:Images/NewtonSystemMod_gr_12.gif]](/images/maths/numerical-analysis/nonlinear/fixed-iterate/NewtonSystemMod_gr_12.gif)
![[Graphics:Images/NewtonSystemMod_gr_13.gif]](/images/maths/numerical-analysis/nonlinear/fixed-iterate/NewtonSystemMod_gr_13.gif)
Suppose that the values of these functions in are known at the point
![[Graphics:Images/NewtonSystemMod_gr_14.gif]](/images/maths/numerical-analysis/nonlinear/fixed-iterate/NewtonSystemMod_gr_14.gif) and we wish to predict their value at a nearby point
and we wish to predict their value at a nearby point
![[Graphics:Images/NewtonSystemMod_gr_15.gif]](/images/maths/numerical-analysis/nonlinear/fixed-iterate/NewtonSystemMod_gr_15.gif) .Let .Let![[Graphics:Images/NewtonSystemMod_gr_16.gif]](/images/maths/numerical-analysis/nonlinear/fixed-iterate/NewtonSystemMod_gr_16.gif) ,denote
differential changes in the dependent variables and , and ,denote
differential changes in the dependent variables and , and![[Graphics:Images/NewtonSystemMod_gr_17.gif]](/images/maths/numerical-analysis/nonlinear/fixed-iterate/NewtonSystemMod_gr_17.gif) denote
differential changes in the independent variables. These changes obey the
relationships denote
differential changes in the independent variables. These changes obey the
relationships
![[Graphics:Images/NewtonSystemMod_gr_18.gif]](/images/maths/numerical-analysis/nonlinear/fixed-iterate/NewtonSystemMod_gr_18.gif) , ,
![[Graphics:Images/NewtonSystemMod_gr_19.gif]](/images/maths/numerical-analysis/nonlinear/fixed-iterate/NewtonSystemMod_gr_19.gif) , ,
![[Graphics:Images/NewtonSystemMod_gr_20.gif]](/images/maths/numerical-analysis/nonlinear/fixed-iterate/NewtonSystemMod_gr_20.gif) . .
If vector notation is used, then this can be
compactly written by using the Jacobian matrix. The function changes aredFand
the changes in the variables are denoteddX.
![[Graphics:Images/NewtonSystemMod_gr_21.gif]](/images/maths/numerical-analysis/nonlinear/fixed-iterate/NewtonSystemMod_gr_21.gif)
or
![[Graphics:Images/NewtonSystemMod_gr_22.gif]](/images/maths/numerical-analysis/nonlinear/fixed-iterate/NewtonSystemMod_gr_22.gif) . .
Convergence near a Fixed
Point
In solving for solutions of a system of equations, iteration is used.We
now turn to the study of sufficient conditions which will guarantee convergence.
Definition (Fixed Point).A
fixed point for
the system of two equations
![[Graphics:Images/NewtonSystemMod_gr_23.gif]](/images/maths/numerical-analysis/nonlinear/fixed-iterate/NewtonSystemMod_gr_23.gif) , ,
![[Graphics:Images/NewtonSystemMod_gr_24.gif]](/images/maths/numerical-analysis/nonlinear/fixed-iterate/NewtonSystemMod_gr_24.gif) . .
is a point
![[Graphics:Images/NewtonSystemMod_gr_25.gif]](/images/maths/numerical-analysis/nonlinear/fixed-iterate/NewtonSystemMod_gr_25.gif) such that
such that
![[Graphics:Images/NewtonSystemMod_gr_26.gif]](/images/maths/numerical-analysis/nonlinear/fixed-iterate/NewtonSystemMod_gr_26.gif) .Similarly,
in three dimensions a
fixed point for the system of three
equations .Similarly,
in three dimensions a
fixed point for the system of three
equations
![[Graphics:Images/NewtonSystemMod_gr_27.gif]](/images/maths/numerical-analysis/nonlinear/fixed-iterate/NewtonSystemMod_gr_27.gif) , ,
![[Graphics:Images/NewtonSystemMod_gr_28.gif]](/images/maths/numerical-analysis/nonlinear/fixed-iterate/NewtonSystemMod_gr_28.gif) , ,
![[Graphics:Images/NewtonSystemMod_gr_29.gif]](/images/maths/numerical-analysis/nonlinear/fixed-iterate/NewtonSystemMod_gr_29.gif) . .
is a point
![[Graphics:Images/NewtonSystemMod_gr_30.gif]](/images/maths/numerical-analysis/nonlinear/fixed-iterate/NewtonSystemMod_gr_30.gif) such that
such that
![[Graphics:Images/NewtonSystemMod_gr_31.gif]](/images/maths/numerical-analysis/nonlinear/fixed-iterate/NewtonSystemMod_gr_31.gif) . .
Definition (Fixed Point
Iteration).For a system of two
equations, fixed point
iteration is
![[Graphics:Images/NewtonSystemMod_gr_32.gif]](/images/maths/numerical-analysis/nonlinear/fixed-iterate/NewtonSystemMod_gr_32.gif) ,and ,and
![[Graphics:Images/NewtonSystemMod_gr_33.gif]](/images/maths/numerical-analysis/nonlinear/fixed-iterate/NewtonSystemMod_gr_33.gif) , ,![[Graphics:Images/NewtonSystemMod_gr_34.gif]](/images/maths/numerical-analysis/nonlinear/fixed-iterate/NewtonSystemMod_gr_34.gif)
Similarly, for a system of three equations,
fixed point iteration
is
![[Graphics:Images/NewtonSystemMod_gr_35.gif]](/images/maths/numerical-analysis/nonlinear/fixed-iterate/NewtonSystemMod_gr_35.gif)
![[Graphics:Images/NewtonSystemMod_gr_36.gif]](/images/maths/numerical-analysis/nonlinear/fixed-iterate/NewtonSystemMod_gr_36.gif) ,and ,and
![[Graphics:Images/NewtonSystemMod_gr_37.gif]](/images/maths/numerical-analysis/nonlinear/fixed-iterate/NewtonSystemMod_gr_37.gif) , ,![[Graphics:Images/NewtonSystemMod_gr_38.gif]](/images/maths/numerical-analysis/nonlinear/fixed-iterate/NewtonSystemMod_gr_38.gif)
Theorem (Fixed-Point
Iteration).Assume that all the
functions and their first partial derivatives are continuous on a region that
contains the fixed point
![[Graphics:Images/NewtonSystemMod_gr_39.gif]](/images/maths/numerical-analysis/nonlinear/fixed-iterate/NewtonSystemMod_gr_39.gif) or
or
![[Graphics:Images/NewtonSystemMod_gr_40.gif]](/images/maths/numerical-analysis/nonlinear/fixed-iterate/NewtonSystemMod_gr_40.gif) ,
respectively.If the starting point is chosen sufficiently close to the fixed
point, then one of the following cases apply. ,
respectively.If the starting point is chosen sufficiently close to the fixed
point, then one of the following cases apply.
Case (i)Two dimensions.If
![[Graphics:Images/NewtonSystemMod_gr_41.gif]](/images/maths/numerical-analysis/nonlinear/fixed-iterate/NewtonSystemMod_gr_41.gif) is sufficiently close to
is sufficiently close to
![[Graphics:Images/NewtonSystemMod_gr_42.gif]](/images/maths/numerical-analysis/nonlinear/fixed-iterate/NewtonSystemMod_gr_42.gif) and if
and if![[Graphics:Images/NewtonSystemMod_gr_43.gif]](/images/maths/numerical-analysis/nonlinear/fixed-iterate/NewtonSystemMod_gr_43.gif)
![[Graphics:Images/NewtonSystemMod_gr_44.gif]](/images/maths/numerical-analysis/nonlinear/fixed-iterate/NewtonSystemMod_gr_44.gif) , ,
![[Graphics:Images/NewtonSystemMod_gr_45.gif]](/images/maths/numerical-analysis/nonlinear/fixed-iterate/NewtonSystemMod_gr_45.gif) , ,
then fixed point iteration will converge to the fixed point
![[Graphics:Images/NewtonSystemMod_gr_46.gif]](/images/maths/numerical-analysis/nonlinear/fixed-iterate/NewtonSystemMod_gr_46.gif) . .
Case (ii)Three
dimensions.If
![[Graphics:Images/NewtonSystemMod_gr_47.gif]](/images/maths/numerical-analysis/nonlinear/fixed-iterate/NewtonSystemMod_gr_47.gif) is sufficiently close to
is sufficiently close to
![[Graphics:Images/NewtonSystemMod_gr_48.gif]](/images/maths/numerical-analysis/nonlinear/fixed-iterate/NewtonSystemMod_gr_48.gif) and if
and if
![[Graphics:Images/NewtonSystemMod_gr_49.gif]](/images/maths/numerical-analysis/nonlinear/fixed-iterate/NewtonSystemMod_gr_49.gif) +
+
![[Graphics:Images/NewtonSystemMod_gr_50.gif]](/images/maths/numerical-analysis/nonlinear/fixed-iterate/NewtonSystemMod_gr_50.gif) +
+
![[Graphics:Images/NewtonSystemMod_gr_51.gif]](/images/maths/numerical-analysis/nonlinear/fixed-iterate/NewtonSystemMod_gr_51.gif) < 1,
< 1,
![[Graphics:Images/NewtonSystemMod_gr_52.gif]](/images/maths/numerical-analysis/nonlinear/fixed-iterate/NewtonSystemMod_gr_52.gif) +
+
![[Graphics:Images/NewtonSystemMod_gr_53.gif]](/images/maths/numerical-analysis/nonlinear/fixed-iterate/NewtonSystemMod_gr_53.gif) +
+
![[Graphics:Images/NewtonSystemMod_gr_54.gif]](/images/maths/numerical-analysis/nonlinear/fixed-iterate/NewtonSystemMod_gr_54.gif) < 1,
< 1,
![[Graphics:Images/NewtonSystemMod_gr_55.gif]](/images/maths/numerical-analysis/nonlinear/fixed-iterate/NewtonSystemMod_gr_55.gif) +
+
![[Graphics:Images/NewtonSystemMod_gr_56.gif]](/images/maths/numerical-analysis/nonlinear/fixed-iterate/NewtonSystemMod_gr_56.gif) +
+
![[Graphics:Images/NewtonSystemMod_gr_57.gif]](/images/maths/numerical-analysis/nonlinear/fixed-iterate/NewtonSystemMod_gr_57.gif) < 1,
< 1,
then fixed point iteration will converge to the fixed point
![[Graphics:Images/NewtonSystemMod_gr_58.gif]](/images/maths/numerical-analysis/nonlinear/fixed-iterate/NewtonSystemMod_gr_58.gif) . .
If these conditions are not met, the iteration might diverge, which is
usually the case.
ProofNonlinear
SystemsNonlinear
Systems
Algorithm (Fixed Point Iteration for Non-Linear
Systems) In two dimensions, solve the non-linear fixed point system
![[Graphics:Images/NewtonSystemMod_gr_59.gif]](/images/maths/numerical-analysis/nonlinear/fixed-iterate/NewtonSystemMod_gr_59.gif)
given one initial approximation
![[Graphics:Images/NewtonSystemMod_gr_60.gif]](/images/maths/numerical-analysis/nonlinear/fixed-iterate/NewtonSystemMod_gr_60.gif) ,
and generating a sequence ,
and generating a sequence
![[Graphics:Images/NewtonSystemMod_gr_61.gif]](/images/maths/numerical-analysis/nonlinear/fixed-iterate/NewtonSystemMod_gr_61.gif) which converges to the solution
which converges to the solution![[Graphics:Images/NewtonSystemMod_gr_62.gif]](/images/maths/numerical-analysis/nonlinear/fixed-iterate/NewtonSystemMod_gr_62.gif) ,i.e. ,i.e.
![[Graphics:Images/NewtonSystemMod_gr_63.gif]](/images/maths/numerical-analysis/nonlinear/fixed-iterate/NewtonSystemMod_gr_63.gif)
Algorithm (Fixed Point Iteration for Non-Linear
Systems)In three dimensions,
solve the non-linear fixed point system
![[Graphics:Images/NewtonSystemMod_gr_64.gif]](/images/maths/numerical-analysis/nonlinear/fixed-iterate/NewtonSystemMod_gr_64.gif)
given one initial approximation
![[Graphics:Images/NewtonSystemMod_gr_65.gif]](/images/maths/numerical-analysis/nonlinear/fixed-iterate/NewtonSystemMod_gr_65.gif) ,
and generating a sequence ,
and generating a sequence
![[Graphics:Images/NewtonSystemMod_gr_66.gif]](/images/maths/numerical-analysis/nonlinear/fixed-iterate/NewtonSystemMod_gr_66.gif) which converges to the solution
which converges to the solution![[Graphics:Images/NewtonSystemMod_gr_67.gif]](/images/maths/numerical-analysis/nonlinear/fixed-iterate/NewtonSystemMod_gr_67.gif) ,i.e. ,i.e.
![[Graphics:Images/NewtonSystemMod_gr_68.gif]](/images/maths/numerical-analysis/nonlinear/fixed-iterate/NewtonSystemMod_gr_68.gif)
Algorithm (Fixed Point Iteration for Non-Linear
Systems)Solve the non-linear
fixed point system
![[Graphics:Images/NewtonSystemMod_gr_69.gif]](/images/maths/numerical-analysis/nonlinear/fixed-iterate/NewtonSystemMod_gr_69.gif) , ,
given one initial approximation
![[Graphics:Images/NewtonSystemMod_gr_70.gif]](/images/maths/numerical-analysis/nonlinear/fixed-iterate/NewtonSystemMod_gr_70.gif) ,
and generating a sequence ,
and generating a sequence
![[Graphics:Images/NewtonSystemMod_gr_71.gif]](/images/maths/numerical-analysis/nonlinear/fixed-iterate/NewtonSystemMod_gr_71.gif) which converges to the solution
which converges to the solution![[Graphics:Images/NewtonSystemMod_gr_72.gif]](/images/maths/numerical-analysis/nonlinear/fixed-iterate/NewtonSystemMod_gr_72.gif) , ,
![[Graphics:Images/NewtonSystemMod_gr_73.gif]](/images/maths/numerical-analysis/nonlinear/fixed-iterate/NewtonSystemMod_gr_73.gif) . .
Remark. First we give a subroutine for
performing fixed point iteration.
Computer ProgramsNonlinear
SystemsNonlinear
Systems
Mathematica Subroutine (Fixed Point Iteration in
n-Dimensions).
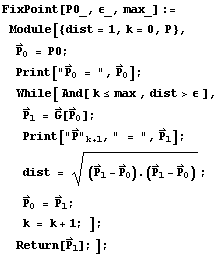
Example 1.Use fixed point iteration to
find a solution to the nonlinear system
![[Graphics:Images/NewtonSystemMod_gr_75.gif]](/images/maths/numerical-analysis/nonlinear/fixed-iterate/NewtonSystemMod_gr_75.gif)
Solution 1.
Newton's Method for Nonlinear
Systems
We now outline the derivation of Newton�s method in two
dimensions.Newton�s method can easily be extended to higher
dimensions.Consider the system
![[Graphics:Images/NewtonSystemMod_gr_186.gif]](/images/maths/numerical-analysis/nonlinear/fixed-iterate/NewtonSystemMod_gr_186.gif)
(1)
![[Graphics:Images/NewtonSystemMod_gr_187.gif]](/images/maths/numerical-analysis/nonlinear/fixed-iterate/NewtonSystemMod_gr_187.gif)
which can be considered a transformation from thexy-plane to the uv-plane.We
are interested in the behavior of this transformation near the point
![[Graphics:Images/NewtonSystemMod_gr_188.gif]](/images/maths/numerical-analysis/nonlinear/fixed-iterate/NewtonSystemMod_gr_188.gif) whose image is the point
whose image is the point
![[Graphics:Images/NewtonSystemMod_gr_189.gif]](/images/maths/numerical-analysis/nonlinear/fixed-iterate/NewtonSystemMod_gr_189.gif) .If
the two functions have continuous partial derivatives, then the differential can
be used to write a system of linear approximations that is valid near the point .If
the two functions have continuous partial derivatives, then the differential can
be used to write a system of linear approximations that is valid near the point
![[Graphics:Images/NewtonSystemMod_gr_190.gif]](/images/maths/numerical-analysis/nonlinear/fixed-iterate/NewtonSystemMod_gr_190.gif) : :
![[Graphics:Images/NewtonSystemMod_gr_191.gif]](/images/maths/numerical-analysis/nonlinear/fixed-iterate/NewtonSystemMod_gr_191.gif)
then substitute the changes
![[Graphics:Images/NewtonSystemMod_gr_192.gif]](/images/maths/numerical-analysis/nonlinear/fixed-iterate/NewtonSystemMod_gr_192.gif) for for![[Graphics:Images/NewtonSystemMod_gr_193.gif]](/images/maths/numerical-analysis/nonlinear/fixed-iterate/NewtonSystemMod_gr_193.gif) ,respectively.Then
we will have ,respectively.Then
we will have
![[Graphics:Images/NewtonSystemMod_gr_194.gif]](/images/maths/numerical-analysis/nonlinear/fixed-iterate/NewtonSystemMod_gr_194.gif) or or
(2)
![[Graphics:Images/NewtonSystemMod_gr_195.gif]](/images/maths/numerical-analysis/nonlinear/fixed-iterate/NewtonSystemMod_gr_195.gif) . .
Consider the system (1) with u and v set
equal to zero,
![[Graphics:Images/NewtonSystemMod_gr_196.gif]](/images/maths/numerical-analysis/nonlinear/fixed-iterate/NewtonSystemMod_gr_196.gif)
(3)
![[Graphics:Images/NewtonSystemMod_gr_197.gif]](/images/maths/numerical-analysis/nonlinear/fixed-iterate/NewtonSystemMod_gr_197.gif)
Suppose we are trying to find the solution
![[Graphics:Images/NewtonSystemMod_gr_198.gif]](/images/maths/numerical-analysis/nonlinear/fixed-iterate/NewtonSystemMod_gr_198.gif) and we start iteration at the nearby point
and we start iteration at the nearby point
![[Graphics:Images/NewtonSystemMod_gr_199.gif]](/images/maths/numerical-analysis/nonlinear/fixed-iterate/NewtonSystemMod_gr_199.gif) ,
then we can apply (2) and write ,
then we can apply (2) and write
![[Graphics:Images/NewtonSystemMod_gr_200.gif]](/images/maths/numerical-analysis/nonlinear/fixed-iterate/NewtonSystemMod_gr_200.gif) . .
Since
![[Graphics:Images/NewtonSystemMod_gr_201.gif]](/images/maths/numerical-analysis/nonlinear/fixed-iterate/NewtonSystemMod_gr_201.gif) ,
this becomes ,
this becomes
![[Graphics:Images/NewtonSystemMod_gr_202.gif]](/images/maths/numerical-analysis/nonlinear/fixed-iterate/NewtonSystemMod_gr_202.gif) , ,
or
![[Graphics:Images/NewtonSystemMod_gr_203.gif]](/images/maths/numerical-analysis/nonlinear/fixed-iterate/NewtonSystemMod_gr_203.gif) . .
When we solve this latter equation for![[Graphics:Images/NewtonSystemMod_gr_204.gif]](/images/maths/numerical-analysis/nonlinear/fixed-iterate/NewtonSystemMod_gr_204.gif) we
get we
get![[Graphics:Images/NewtonSystemMod_gr_205.gif]](/images/maths/numerical-analysis/nonlinear/fixed-iterate/NewtonSystemMod_gr_205.gif) and the next approximation
and the next approximation
![[Graphics:Images/NewtonSystemMod_gr_206.gif]](/images/maths/numerical-analysis/nonlinear/fixed-iterate/NewtonSystemMod_gr_206.gif) is
is
![[Graphics:Images/NewtonSystemMod_gr_207.gif]](/images/maths/numerical-analysis/nonlinear/fixed-iterate/NewtonSystemMod_gr_207.gif)
Theorem
(Newton-Raphson Method for 2-dimensional Systems).To
solve the non-linear system
![[Graphics:Images/NewtonSystemMod_gr_208.gif]](/images/maths/numerical-analysis/nonlinear/fixed-iterate/NewtonSystemMod_gr_208.gif) , ,
given one initial approximation
![[Graphics:Images/NewtonSystemMod_gr_209.gif]](/images/maths/numerical-analysis/nonlinear/fixed-iterate/NewtonSystemMod_gr_209.gif) ,
and generating a sequence ,
and generating a sequence
![[Graphics:Images/NewtonSystemMod_gr_210.gif]](/images/maths/numerical-analysis/nonlinear/fixed-iterate/NewtonSystemMod_gr_210.gif) which converges to the solution
which converges to the solution
![[Graphics:Images/NewtonSystemMod_gr_211.gif]](/images/maths/numerical-analysis/nonlinear/fixed-iterate/NewtonSystemMod_gr_211.gif) ,i.e. ,i.e.
![[Graphics:Images/NewtonSystemMod_gr_212.gif]](/images/maths/numerical-analysis/nonlinear/fixed-iterate/NewtonSystemMod_gr_212.gif) . .
Suppose that![[Graphics:Images/NewtonSystemMod_gr_213.gif]](/images/maths/numerical-analysis/nonlinear/fixed-iterate/NewtonSystemMod_gr_213.gif) has been obtained, use the following steps to obtain
has been obtained, use the following steps to obtain
![[Graphics:Images/NewtonSystemMod_gr_214.gif]](/images/maths/numerical-analysis/nonlinear/fixed-iterate/NewtonSystemMod_gr_214.gif) . .
Step 1.Evaluate the function![[Graphics:Images/NewtonSystemMod_gr_215.gif]](/images/maths/numerical-analysis/nonlinear/fixed-iterate/NewtonSystemMod_gr_215.gif) . .
Step 2.Evaluate the Jacobian![[Graphics:Images/NewtonSystemMod_gr_216.gif]](/images/maths/numerical-analysis/nonlinear/fixed-iterate/NewtonSystemMod_gr_216.gif) . .
Step 3.Solve the linear system![[Graphics:Images/NewtonSystemMod_gr_217.gif]](/images/maths/numerical-analysis/nonlinear/fixed-iterate/NewtonSystemMod_gr_217.gif) for for![[Graphics:Images/NewtonSystemMod_gr_218.gif]](/images/maths/numerical-analysis/nonlinear/fixed-iterate/NewtonSystemMod_gr_218.gif) . .
Step 4.Compute the next approximation![[Graphics:Images/NewtonSystemMod_gr_219.gif]](/images/maths/numerical-analysis/nonlinear/fixed-iterate/NewtonSystemMod_gr_219.gif) . .
Mathematica Subroutine (Newton's Method for Systems
in n-Dimensions).
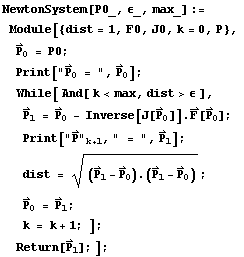
|

