Example(b).
Consider
the function![[Graphics:Images/HalleysMethodMod_gr_61.gif]](/images/maths/numerical-analysis/nonlinear/halley-sol-2/HalleysMethodMod_gr_61.gif) ,
which has a root at ,
which has a root at![[Graphics:Images/HalleysMethodMod_gr_62.gif]](/images/maths/numerical-analysis/nonlinear/halley-sol-2/HalleysMethodMod_gr_62.gif) . .
1 (b).Use
Halley's formula to find the root.Use the starting value![[Graphics:Images/HalleysMethodMod_gr_64.gif]](/images/maths/numerical-analysis/nonlinear/halley-sol-2/HalleysMethodMod_gr_64.gif)
Solution 1 (b).
Now we will investigate Halley's iteration
for finding square roots.
![[Graphics:../Images/HalleysMethodMod_gr_126.gif]](/images/maths/numerical-analysis/nonlinear/halley-sol-2/HalleysMethodMod_gr_126.gif)
![[Graphics:../Images/HalleysMethodMod_gr_127.gif]](/images/maths/numerical-analysis/nonlinear/halley-sol-2/HalleysMethodMod_gr_127.gif)
Form the Halley iteration functionh(x).
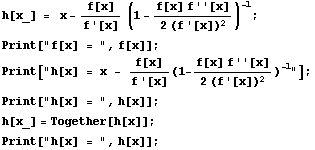
![[Graphics:../Images/HalleysMethodMod_gr_129.gif]](/images/maths/numerical-analysis/nonlinear/halley-sol-2/HalleysMethodMod_gr_129.gif)
![[Graphics:../Images/HalleysMethodMod_gr_130.gif]](/images/maths/numerical-analysis/nonlinear/halley-sol-2/HalleysMethodMod_gr_130.gif)
![[Graphics:../Images/HalleysMethodMod_gr_131.gif]](/images/maths/numerical-analysis/nonlinear/halley-sol-2/HalleysMethodMod_gr_131.gif)
![[Graphics:../Images/HalleysMethodMod_gr_132.gif]](/images/maths/numerical-analysis/nonlinear/halley-sol-2/HalleysMethodMod_gr_132.gif)
We start the iteration with![[Graphics:../Images/HalleysMethodMod_gr_133.gif]](/images/maths/numerical-analysis/nonlinear/halley-sol-2/HalleysMethodMod_gr_133.gif) and
carry 100 digits in the computations, by
telling Mathematica the precision of and
carry 100 digits in the computations, by
telling Mathematica the precision of
![[Graphics:../Images/HalleysMethodMod_gr_134.gif]](/images/maths/numerical-analysis/nonlinear/halley-sol-2/HalleysMethodMod_gr_134.gif) by issuing the command p[0] = N[2,100].Next,
a short program is written to compute the first five terms in the iteration:
by issuing the command p[0] = N[2,100].Next,
a short program is written to compute the first five terms in the iteration:
![[Graphics:../Images/HalleysMethodMod_gr_135.gif]](/images/maths/numerical-analysis/nonlinear/halley-sol-2/HalleysMethodMod_gr_135.gif)
![[Graphics:../Images/HalleysMethodMod_gr_136.gif]](/images/maths/numerical-analysis/nonlinear/halley-sol-2/HalleysMethodMod_gr_136.gif)
![[Graphics:../Images/HalleysMethodMod_gr_137.gif]](/images/maths/numerical-analysis/nonlinear/halley-sol-2/HalleysMethodMod_gr_137.gif)
![[Graphics:../Images/HalleysMethodMod_gr_138.gif]](/images/maths/numerical-analysis/nonlinear/halley-sol-2/HalleysMethodMod_gr_138.gif)
![[Graphics:../Images/HalleysMethodMod_gr_139.gif]](/images/maths/numerical-analysis/nonlinear/halley-sol-2/HalleysMethodMod_gr_139.gif)
![[Graphics:../Images/HalleysMethodMod_gr_140.gif]](/images/maths/numerical-analysis/nonlinear/halley-sol-2/HalleysMethodMod_gr_140.gif)
![[Graphics:../Images/HalleysMethodMod_gr_141.gif]](/images/maths/numerical-analysis/nonlinear/halley-sol-2/HalleysMethodMod_gr_141.gif)
Since the root is known to be exactly![[Graphics:../Images/HalleysMethodMod_gr_142.gif]](/images/maths/numerical-analysis/nonlinear/halley-sol-2/HalleysMethodMod_gr_142.gif) we
can have Mathematica list the error we
can have Mathematica list the error![[Graphics:../Images/HalleysMethodMod_gr_143.gif]](/images/maths/numerical-analysis/nonlinear/halley-sol-2/HalleysMethodMod_gr_143.gif) at
each step in the iteration: at
each step in the iteration:
![[Graphics:../Images/HalleysMethodMod_gr_144.gif]](/images/maths/numerical-analysis/nonlinear/halley-sol-2/HalleysMethodMod_gr_144.gif)
![[Graphics:../Images/HalleysMethodMod_gr_145.gif]](/images/maths/numerical-analysis/nonlinear/halley-sol-2/HalleysMethodMod_gr_145.gif)
![[Graphics:../Images/HalleysMethodMod_gr_146.gif]](/images/maths/numerical-analysis/nonlinear/halley-sol-2/HalleysMethodMod_gr_146.gif)
![[Graphics:../Images/HalleysMethodMod_gr_147.gif]](/images/maths/numerical-analysis/nonlinear/halley-sol-2/HalleysMethodMod_gr_147.gif)
![[Graphics:../Images/HalleysMethodMod_gr_148.gif]](/images/maths/numerical-analysis/nonlinear/halley-sol-2/HalleysMethodMod_gr_148.gif)
![[Graphics:../Images/HalleysMethodMod_gr_149.gif]](/images/maths/numerical-analysis/nonlinear/halley-sol-2/HalleysMethodMod_gr_149.gif)
Looking at the error, we see that the number
of accurate digits is tripling at each step in the computations, hence
convergence is proceeding cubically.
We can conclude that Halley's method is faster than Newton's method.
Verify the convergence rate.At the
simple root![[Graphics:../Images/HalleysMethodMod_gr_150.gif]](/images/maths/numerical-analysis/nonlinear/halley-sol-2/HalleysMethodMod_gr_150.gif) we
can explore the ratio we
can explore the ratio
![[Graphics:../Images/HalleysMethodMod_gr_151.gif]](/images/maths/numerical-analysis/nonlinear/halley-sol-2/HalleysMethodMod_gr_151.gif) . .
![[Graphics:../Images/HalleysMethodMod_gr_152.gif]](/images/maths/numerical-analysis/nonlinear/halley-sol-2/HalleysMethodMod_gr_152.gif)
Therefore, the Halley iteration is converging cubically.
Back.
|