Boundary Conditions of a Typical Partial Differential Equation in Two Dimensions
For the purpose of simplicity, we shall start our consideration with partial
differential equations in only two variables and linear in the second
derivatives. Such equations have the general form
Such an equation is called a quasilinear second order partial differential
equation. If the expression
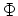where linear in
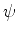, i.e., if
then the equation would be a linear p.d.e., but this need not be the case.
The equation has a nondenumerable infinity of solution. In order to single
out a unique solution, the to-be-found function
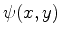must satisfy additional conditions. They are usually specified at the boundary
of the domain of the p.d.e.
In three dimensional space, this boundary is a surface, but in our two
dimensional case, we have a boundary line which can be specified by the
parametrized curve
where
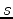is the arclength parameter
The tangent to this curve has components
They satisfy
The normal to this boundary curve has components
We assume that
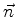points towards the interior of the domain where the solution is to be
found. If this is not the case, we reverse the signs of the components of it.
The additional conditions which the to-be-found solution
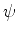is to satisfy are imposed at this boundary curve, and they are conditions on the
partial derivatives and the value of the function
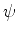evaluated at the curve.
The boundary curve accomodates three important types of boundary conditions.
- Dirichlet conditions:
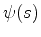is specified at each point of the boundary.
- Neumann conditions:
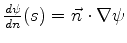 , the normal componet
of the graident of
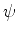is specified at each point of the boundary.
- Cauchy conditions:
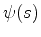and
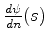are specified at each point of the boundary. The parameter
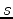is usually a time parameter. Consequently, Cauchy conditions are also called
intial value conditions or initial value data or simply
Cauchy data.
There exists also the mixed Dirichlet-Neumann conditions. They are
intermediate between the Dirichlet and the Neumann boundary conditions, and they
are given by
Here
,
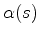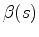, and
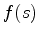are understood to be given on the boundary.
We recall that in the theory of ordinary second order differential equations,
a unique solution was obtained once the solution and its derivative were
specified at a point. The generalization of this condition to partial
differential equations consists of the Cauchy boundary conditions.
Consequently, we now inquire whether the solution of the partial differential
equation is uniquely determined by specifying Cauchy boundary conditions on the
boundary
.
|
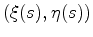