Cauchy Problem and Characteristics
In order to compute the function
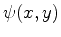at points off the boundary curve, we resort to the Taylor series on two
dimensions;
Here the derivatives are to be evaluated on the boundary.
The problem we are confronted with is this:
Determine all partial derivatives, starting with the first partials on up
from the given Cauchy boundary conditions, the given boundary, and the given
partial differential equation!
We shall do this first for the first derivatives.
From the Cauchy data we obtain two equations
 |
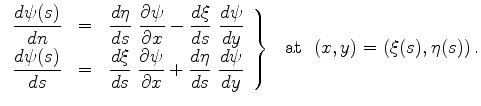(610) |
From these we obtain the first partial derivatives of
evaluates on the boundary
 |
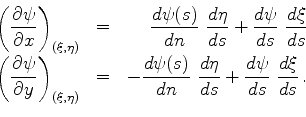(611) |
The procurement of the second derivatives is more interesting. We
differentiate the (known) first derivatives along the boundary. Together with
the given p.d.e. we have
The left hand sides of these three equations are known along the whole
boundary. So are the coefficients of the three unknown partial derivatives on
the right hand side. One can solve for these partial derivatives unless
or
If this determinant does not vanish, one can solve for the second derivatives
evaluated on the boundary. Differentiating along the boundary yields
Subscripts refer to partial derivatives. The last equation was obtained
differentiating the given p.d.e. with respect to
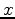. The left hand side contains only lower order derivatives, which are known on
the boundary.
We see that one can solve for
on the boundary unless the determinant, the same one as before, vanishes. It is
evident that one can continue the process of solving for the other higher order
derivatives, provided the determinant of the system does not vanish. We are led
to the conclusion that one can expand
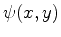in a Taylor series at every point of the boundary and that the coefficients of
the series are uniquely determined by the Cauchy boundary conditions on the
given boundary.
We must now examine the vanishing of the system determinant
 |
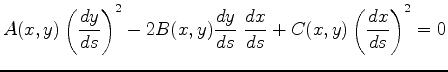(612) |
at every point of the domain of the partial differential equation.
Depending on the coefficients
,
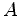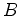, and
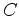, this quadratic form determines two characteristic curves,
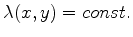and
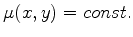, through each point
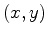. We distinguish between three cases:
-
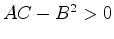: elliptic type in which the two characteristics
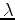and
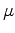are complex conjugates of each other.
-
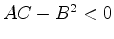: hyperbolic type in which case for each
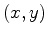the characteristics
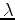and
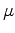are real. They sre two curves intersecting at
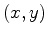. As one varies
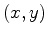one obtains two distinct families.
-
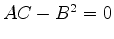: parabolic type in which there is only one family of
characteristics.
These three cases imply three different types of differential equations. By
utilizing the characteristic, one can introduce new coordinates relative to
which a differential equation of each type assumes a standard normal form. Let
the new coordinate surfaces be
Then the coordinate transformation
yields a normal form of the elliptic type,
By contrast the coordinate transformation
yields a normal form of the hyperbolic type,
Finally, the coordinate transformation
yields a normal form of the parabolic type,
We recognize that elliptic partial differential equations express an
equilibrium or a static potential phenomenon.
By introducing the standard coordinates
in terms of which
one finds that
the wave equation of a general vibrating string. We, therefore, recognize that a
hyperbolic p.d. equation expresses the phenomenon of a propagating
wave or disturbance.
Finally, a parabolic p.d. equation expresses a diffusion process. In fact,
the two dimensional Laplace equation, the equation for a vibrating
sting, and the heat conduction equation are the simplest possible
examples of elliptic, hyperoblic, and parabolic equations.
|
![$\displaystyle +\frac{1}{2!}\left[ (x-\xi )^2\frac{\partial^2\psi}{\partial x^2}...
...l x\partial y} +(y-\xi )^2
\frac{\partial^2\psi}{\partial y^2}\right]+\cdots\,.$](/images/maths/partial-differential/cauchy/img4045.png)
