Cylindrical Coordinates

Cylindrical Coordinates

The benefits of the linear algebra viewpoint applied to Maxwell's equations can be extended by inspection from rectilinear cartesian to cylindrical coordinates. This is because the four-dimensional coordinate system lends itself to being decomposed into two orthogonal sets of coordinate surfaces. For cylindricals these are spanned by the transverse coordinates 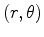in the transverse plane, and the longitudinal coordinates 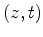in the longitudinal plane.

The transition from a rectilinear to a cylindrical coordinate frame is based on the replacement of the following symbols:

		(677)
		(678)
and
		(679)

Such a replacement yields the vector field components relative to an orthonormal (o.n.) basis tangent to the coordinate lines. To emphasize this orthonormality, hats (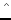 ) are placed over the vector components.

This replacement is very powerful. It circumvents the necessity of having to repeat the previous calculations that went into exhibiting the individual components of Maxwell's 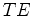, , 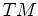and 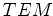systems of equations. We shall again take advantage of the power of this algorithm in the next section when we apply it to Maxwell's system relative to spherical coordinates.

Applying it within the context of cylindrical coordinates, one finds that the source and the vector potential four-vectors are as follows:

1. for a 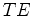source

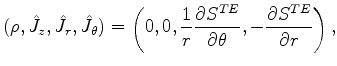   (680)

   
    

   the solution to the Maxwell field equations has the form

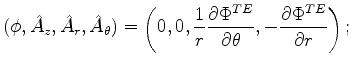   (681)

   
    

    

2. for a 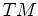source

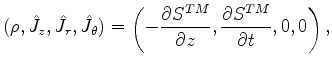   (682)

   
    

   the solution to the Maxwell field equations has the form

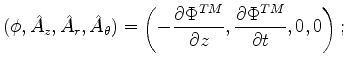   (683)

   
    

   and

3. for a source

   (684)

   
    

   the solution to the Maxwell field equations has the form

   (685)