Hyperbolic Equations
The quadratic form, Eq.(6.12),
determined by the coefficients
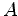 ,
,
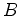 , and
, and
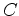 of the given p.d.e. can be factored into two ordinary differential equation
of the given p.d.e. can be factored into two ordinary differential equation
These are the equations for the two families of characteristic curves of
the given p.d.e.
Their significance, we recall, is this: if the boundary line coincides with
one of them, then specifying Cauchy data on it will not yield a unique
solution. If, however, the boundary line intersects each family only once, then
the Cauchy data will yields a unique solution.
This point becomes particularly transparent if one introduces the curvilinear
coordinates
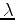 and
and
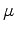 relative to which the given p.d.e. assumes its standard form, Eq.(>6.13).
We shall consider the hyperbolic case by assuming that
relative to which the given p.d.e. assumes its standard form, Eq.(>6.13).
We shall consider the hyperbolic case by assuming that
throughout the
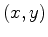 domain.
domain.
We shall demand the new coordinates
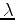 and
and
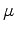 - the characteristic coordinates - have the property that their isograms
(``loci of points of constant values'') contain the characteristic lines
- the characteristic coordinates - have the property that their isograms
(``loci of points of constant values'') contain the characteristic lines
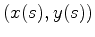 , i.e.,
, i.e.,
for all
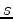 . This implies that
. This implies that
where, as usual
Substituting these equations into Eq.(6.12),
the equation for the characteristic directions, one obtains
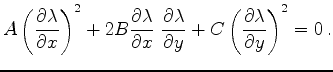 |
|
|
(614) |
An equation with the same coefficients is obtained for the other
function
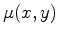 . The two solutions
. The two solutions
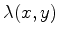 and
and
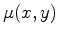 are real valued functions. Their isograms, the characteristics of the
hyperbolic equation, give us the new curvilinear coordinate system
are real valued functions. Their isograms, the characteristics of the
hyperbolic equation, give us the new curvilinear coordinate system
The partial derivatives of the given differential equation are now as follows
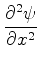
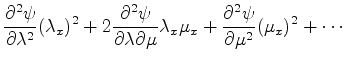
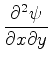
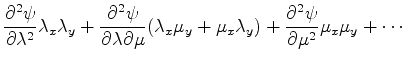
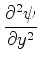
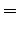
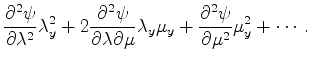
Here
 refers to additional terms involving only the first partial derivatives of
refers to additional terms involving only the first partial derivatives of
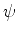 . Inserting these expressions into the given p.d. equation, one obtains
. Inserting these expressions into the given p.d. equation, one obtains
![$\displaystyle [A\lambda^2_x+2B\lambda_x\lambda_y+C\lambda^2_y]\frac{\partial^2\psi}
{\partial\lambda^2}$](/images/maths/partial-differential/hyperbolic/img4098.png)
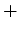
![$\displaystyle [2A\lambda_x\mu_x+B(\lambda_x\mu_y+\mu_x\lambda_y)+
2C\lambda_y\mu_y]\frac{\partial^2\psi}{\partial\lambda\partial\mu}$](/images/maths/partial-differential/hyperbolic/img4099.png)
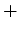
![$\displaystyle [A\mu^2_x+2B\mu_x\mu_y+C\mu^2_y]\frac{\partial^2\psi}{\partial\mu^2}$](/images/maths/partial-differential/hyperbolic/img4100.png)
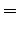
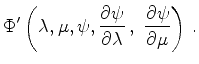 (615) (615)
It follows from Equation
6.14 that the coefficients of
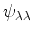 and
and
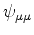 vanish. Solving for
vanish. Solving for
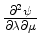 yields Equation
>
6.13, the hyperbolic equation in normal form.
yields Equation
>
6.13, the hyperbolic equation in normal form.
The coordinates
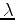 and
and
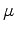 , whose surfaces contain the characteristic lines, are called the
characteristic coordinates or null coordinates of the hyperbolic
equation.
, whose surfaces contain the characteristic lines, are called the
characteristic coordinates or null coordinates of the hyperbolic
equation.
These coordinates are important for at least two reasons. First of all, they
are boundaries across which a solution can be nonanalytic. If
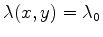 is one of the isograms (``locus of points where
is one of the isograms (``locus of points where
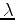 has constant value'') of the solution to Eq.(6.14),
then the first term of the p.d. Eq.(6.15)
has constant value'') of the solution to Eq.(6.14),
then the first term of the p.d. Eq.(6.15)
even if
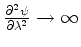 as
as
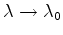 . In other words, there are solutions to Eq.(6.15)
for which the first derivative
. In other words, there are solutions to Eq.(6.15)
for which the first derivative
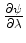 has a discontinuity across the characteristic
has a discontinuity across the characteristic
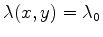 . Similarly, there exist solutions to Eq.(6.15)
whose first derivative
. Similarly, there exist solutions to Eq.(6.15)
whose first derivative
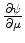 has a discontinuity across
has a discontinuity across
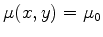 whenever
whenever
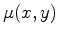 satisfies Eq.(6.14)
with
satisfies Eq.(6.14)
with
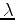 replaced by
replaced by
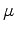 .
.
Secondly, these coordinates depict the history of a moving disturbance. The
simple string illustrates the issue involved.
Example: The Simple string The governing equation is
Its characteristic coordinates are the ``retarded'' and the ``advanced'' times
and its normal form is
The solution is
where
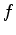 and
and
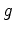 are any functions of
are any functions of
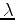 and
and
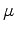 .
.
Next consider the initial value data at
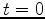 :
:
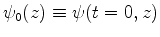
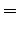

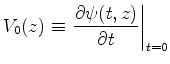
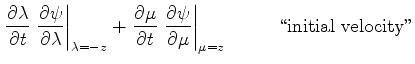
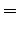
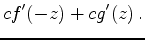
These equations imply
Consider the intersection of the two families of characteristics with the
boundary line
 as in the figure below.
as in the figure below.
Figure 6.1: Characteristic
coordinate lines
 and
and
 as determined by the wave equation for a simple string.
as determined by the wave equation for a simple string.
| |
Note that
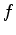 is constant along the
is constant along the
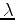 characteristics (i.e., where
characteristics (i.e., where
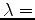 constant), while
constant), while
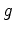 is constant along the
is constant along the
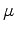 characteristics. It follows that if
characteristics. It follows that if
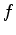 is known on the boundary segment
is known on the boundary segment
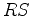 , then
, then
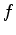 is known along all the
is known along all the
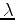 -characteristics intersecting
-characteristics intersecting
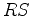 . Similarly, if
. Similarly, if
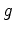 is known along
is known along
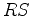 , then
, then
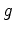 is known along all the
is known along all the
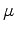 -characteristics intersecting
-characteristics intersecting
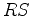 . And this is precisely the case because the Cauchy data on
. And this is precisely the case because the Cauchy data on
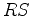 determine the values of both
determine the values of both
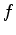 and
and
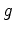 on that segment.
on that segment.
Being the sum of the two functions, the solution to the wave equation is
Thus one sees that any disturbance on a string consists of two parts: one
propagating to the right the other to the left. The propagation speeds are
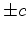 , the slopes of the characteristics relative to the
, the slopes of the characteristics relative to the
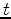 -
-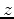 coordinate system. The idiosyncratic aspect of the simple string is that these
two parts do not change their shape as they propagate along the string.
coordinate system. The idiosyncratic aspect of the simple string is that these
two parts do not change their shape as they propagate along the string.
A general linear hyperbolic system does not share this feature. However, what
it does share with a simple string is that its solution is uniquely determined
in the common region traversed by the two sets of characteristics which
intersect
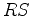 . In fact, the Cauchy data on
. In fact, the Cauchy data on
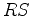 determine a unique solution
determine a unique solution
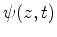 at every point in the region
at every point in the region
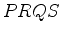 . This is why it is called the domain of dependence of
. This is why it is called the domain of dependence of
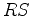 . To justify these claims it is neccessary to construct this unique solution to
a general second order linear hyperbolic differential equation.
. To justify these claims it is neccessary to construct this unique solution to
a general second order linear hyperbolic differential equation.
|

