Maxwell Wave Equation
The first pair of Maxwell's equations, (6.39)
and (6.40),
imply that there exists a vector potential
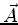 and scalar potential
and scalar potential
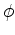 from which one derives the electric and magnetic fields,
from which one derives the electric and magnetic fields,
Conversely, the existence of these potentials guarantees that the first pair of
these equations is satisfied automatically. By applying these potentials to the
differential expressions of the second pair of Maxwell's equations, (6.41-6.42)
one obtains the mapping
![$\displaystyle \left[ \begin{array}{c} \phi\\ \vec A \end{array} \right] ~~\stac...
...leadsto} \mathcal{A}\left[ \begin{array}{c} \phi\\ \vec A \end{array} \right]~,$](/images/maths/partial-differential/maxwell/img4289.png) |
(645) |
where
![$\displaystyle \mathcal{A}\left[ \begin{array}{c} \phi\\ \vec A \end{array} \rig...
...l\phi}{\partial t}+ \frac{\partial^2\vec A}{\partial t^2} \end{array} \right]~.$](/images/maths/partial-differential/maxwell/img4290.png) |
(646) |
It follows that Maxwell's field equations reduce to Maxwell's four-component
wave equation,
![$\displaystyle \left[ \begin{array}{c} \displaystyle -\nabla^2\phi -\nabla \cdot...
...ray} \right] = 4\pi \left[ \begin{array}{c} \rho\\ \vec J \end{array} \right]~.$](/images/maths/partial-differential/maxwell/img4291.png) |
(647) |
Maxwell's wave operator is the linch pin of his theory of electromagnetism. This
is because it has the following properties:
- It is a linear map from the space of four-vector fields into
itself, i.e.
at each point event
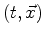 .
.
- The map is singular. This means that there exist nonzero vectors
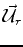 and
and
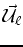 such that
such that
In particular, one has
- the fact that
for all three-times differentiable scalar fields
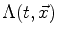 . Thus
. Thus
The null space of
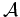 is therefore nontrivial and 1-dimensional at each
is therefore nontrivial and 1-dimensional at each
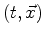 .
.
- the fact that
for all 4-vectors
![$ \left[
\begin{array}{c}
\phi\\
\vec A
\end{array}
\right]$](/images/maths/partial-differential/maxwell/img4305.png) . Thus . Thus
The left null space of
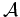 is therefore also 1-dimensional at each
is therefore also 1-dimensional at each
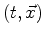 .
.
In light of the singular nature of
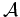 , the four-component Maxwell wave equation
, the four-component Maxwell wave equation
has no solution unless the source
![$ \left[
\begin{array}{c}
\rho\\
\vec J
\end{array}
\right]$](/images/maths/partial-differential/maxwell/img4312.png) also satisfies also satisfies
This is the linear algebra way of expressing
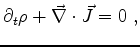 |
(652) |
the differential law of charge conservation. Thus Maxwell's equations apply if
and only if the law of charge conservation holds. If charge conservation did not
hold, then Maxwell's equations would be silent. They would not have a solution.
Such silence is a mathematical way of expressing the fact that at its root
theory is based on observation and established knowledge, and that arbitrary
hypotheses must not contaminate the theoretical.
|