The linear algebra aspects of Maxwell's wave operator
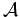are illustrated by the following problem from linear algebra:
-
- Solve
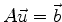for
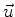, under the stipulation that
The fact that
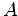is singular and
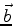belongs to the range of
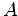makes the system over-determined but consistent. This means that there are
more equations than there are unknowns.
One solves the problem in two steps.
-
-
- Step I:
- Let
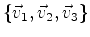 be the set of
eigenvectors having non-zero eigenvalues. Whatever
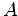is, the task of finding three vectors that satisfy
| |
 |
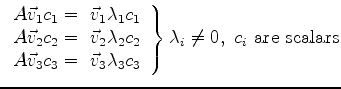(654) |
and
|
| |
 |
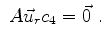(655) |
Being spanned by the three eigenvectors with non-zero eigenvalues, the
range space of
,
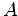is well-determined. However, the scalars
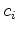are at this stage as yet undetermined.
- Step II:
- Continuing the development, recall that quite generally
and that if
It is appropriate to alert the reader that in the ensuing section the vectors
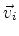and the eigenvalues
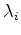become differential operators which act on scalar fields
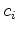and that the three subscript labels will refer to the TE, TM, and TEM
eletromagnetic66
vector potentials respectively.
Equating (6.56)
and (6.57),
one finds that the linear independence of
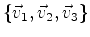implies the following
equations for
,
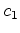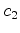, and
:
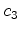Consequently, the solution is
where
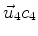is an indeterminate multiple of the null space vector
.
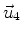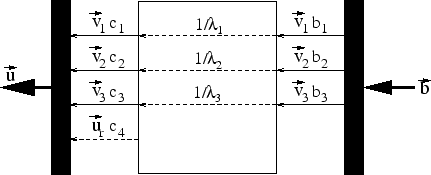
If one represents the stated problem
(
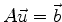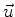determines
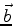) as an input-output process, as in Figure 6.3,
Figure 6.3: The matrix
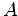defines an input-output process.
 |
then its solution is represented by the inverse input-output process as in
Figure 6.4.
Figure: The solution to
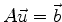defines an inverse input-output process.
 |
In general, the task of finding the eigenvectors of a 4
4 matrix can be a nontrivial task. However, given the fact that the solution to
is already known, one finds that the associated constraints on the eigenvectors,
make the task quite easy, if not trivial.
|
