Riemann's Method for Integrating the Most General 2nd Order Linear
Hyperbolic Equation
In its most general form a linear second order hyperbolic equation is
 |
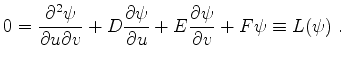(617) |
In compliance with standard practice one designates the characteristic
coordinates by
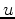and
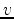. The problem to be solved is this:
Given
(a) the differential Eq.(6.17)
and
(b) the initial value data (=Cauchy conditions)
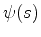and its normal derivative
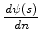on the given curve in Figure
6.2,
Find: the function
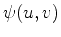which satisfies (a) and (b).
Figure 6.2: Characteristic
coordinates of a hyperbolic differetial equation in two dimensions.
 |
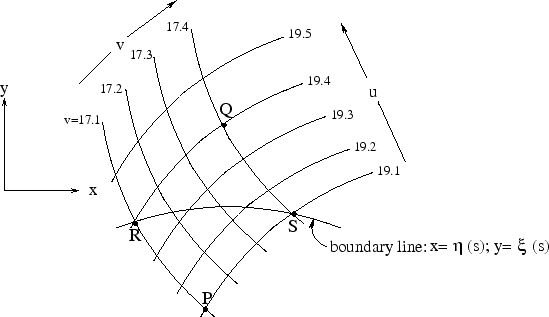Riemann's method of solving this problem is a three-step process whose essence
parallels the Green's function method
|
