Single Partial Differential Equations: Their Origin
There are many phenomena in nature, which, even though occuring over finite
regions of space and time, can be described in terms of properties that prevail
at each point of space and time separately. This description originated with
Newton, who with the aid of his differential calculus showed us how to grasp a
global phenomenon, for example, the elliptic orbit of a planet, by means of a
locally applied law, for example
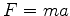 .
.
This manner of making nature comprehensible has been extended from the motion
of single point particles to the behavior of other forms of matter and energy,
be it in the form of gasses, fluids, light, heat, electricity, signals traveling
along optical fibers and neurons, or even gravitation.
This extension consists of formulating or stating a partial differential
equation governing the phenomenon, and then solving that differential equation
for the purpose of predicting measurable properties of the phenomenon.
There exist many partial differential equations, but from the view point of
mathematics, there are basically only three types of partial differential
equations.
They are exemplified by
- Laplaces equation
which governs electrostatic and magnetic fields as well as the velocity
potential of an incompressible fluid, by
- the wave equation
for electromagnetic or sound vibrations, and by
for the vibrations of a simple string, and by
- the diffusion equation
for the temperature in three dimensional space and in time, or by
for the temperature along a uniform rod.
|