One of the chief virtues of the linear algebra viewpoint applied to Maxwell's
equations is that it directs attention to the system's fundamental vector spaces
and their properties. The easiest way to identify them in a computational way
happens when the underlying coordinate system permits a 2+2 decomposition into
what amounts to longitudinal and transverse surfaces. Spherical coordinates
provide a nontrivial example of this. There a transverse surface is a sphere
spanned by
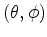, while the longitudinal coordinates are
.
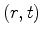The distinguishing feature of spherical coordinates, as compared to
rectilinear or cylindrical coordinates, is that coordinate rectangles on
successive transverse surfaces (nested spheres) are not congruent. Instead, they
have areas that scale with the square of the radial distance from the origin.
This scaling alters the representation of the divergence of a vector field and
hence the Maxwell wave operator. Nevertheless, the eigenvalue method with its
resulting TE-TM-TEM decomposition of the e.m. field readily accomodates these
alterations.
|
