System of Partial Differential Equations: How to Solve Maxwell's Equations
Using Linear Algebra
The theme of the ensuing development is linear algebra, but the subject is an
overdetermined system of partial differential equations, namely, the Maxwell
field equations. The objective is to solve them via the method of eigenvectors
and eigenvalues. The benefit is that the task of solving the Maxwell system of
p.d. equations is reduced to solving a single inhomogeneous scalar equation64
where
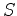 is a time and space dependent source. The impatient reader will find that once
this master equation, or its manifestation in another coordinate system, has
been solved, the electric and magnetic fields are entirely determined as in
Tables
is a time and space dependent source. The impatient reader will find that once
this master equation, or its manifestation in another coordinate system, has
been solved, the electric and magnetic fields are entirely determined as in
Tables ![[*]](/images/maths/partial-differential/system-partial/crossref.png) -6.9. -6.9.
The starting point of the development is Maxwell's equations. There is the
set of four functions, the density of charge
which are usually given. These space and time dependent charge distributions
give rise to electric and magnetic fields,
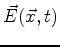 and and
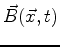 . The relationship is captured by means of Maxwell's gift to twentieth century
science and technology,
. The relationship is captured by means of Maxwell's gift to twentieth century
science and technology,
Maxwell's field equations65.
Exercise 62.1 (Charge Flux-Density of an Isolated Charge)
Microscopic observations show that charged matter is composed of discrete
point charges. On the other hand, macroscopic observations show that charged
matter is the carrier of an electric fluid which is continuous. Dirac delta
functions provide the means to grasp both attributes from a single
perspective. This fact is highlighted by the following problem.
Consider the current-charge density due to an isolated moving charge,
a) Show that this current-charge density satisfies
Remark. The four-vector
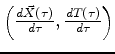 is the charge's four-velocity in spacetime. The parameter
is the charge's four-velocity in spacetime. The parameter
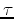 is the ``wristwatch'' time (as measured by a comoving clock) attached to
this charge.
is the ``wristwatch'' time (as measured by a comoving clock) attached to
this charge.
b) By taking advantage of the fact
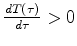 , evaluate the
, evaluate the
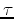 -integrals, and obtain explicit expressions for the components
-integrals, and obtain explicit expressions for the components
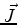 and
and
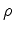 .
.
Answer:
|