Baye's Theorem

Baye's Theorem

In the previous section, we have learnt that

i) If A and B are two mutually exclusive events, then

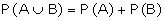
ii)

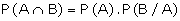
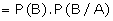
Before we state and prove Baye's Theorem, we use the above two rules to state the law of total probability. The law of total probability is useful in proving Baye's theorem and in solving probability problems. Following is an example which explains this law.

Example:

Let S is the sample space which is the population of adults in a small town who have completed the requirement for a college degree. The population is categorized according to sex and employment status as follows

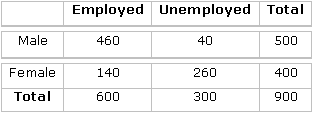
\ One of these individual is to be selected for a tour throughout the country. Knowing that the individual chosen is employed, what is the probability that the individual is a man?

Suggested answer:

Let M be the event that a man is selected, E be the event that the individual selected, is employed. Using the reduced sample space, we have

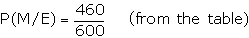
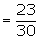
Also, we have

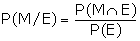
From the original sample space, we have

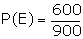
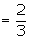
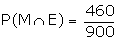
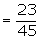
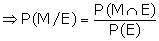
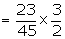
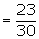
Suppose that we are now given the additional information that 36 of those employed and 12 of these unemployed are the members of the rotary club. What is the probability of the event A that the selected individual is a member of the rotary club?

Suggested answer:

A is the event that the selected individual is a member of the rotary club.

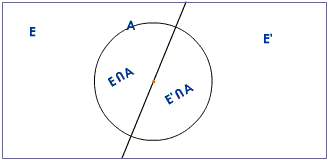
From the figure, it is clear that

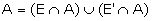
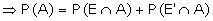
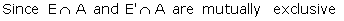
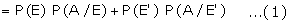
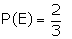
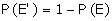
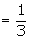
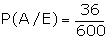
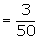
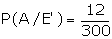
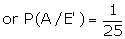
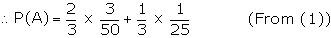
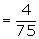
The generalization of the foregoing example, where the sample space is partitioned into n subsets is known as Law of Total Probability. Theorem: (Law of Total Probability) If B₁, B₂, B₃, �.., B_n are mutually exclusive and exhaustive events of the sample space S, then for any event A of S.

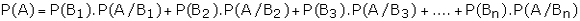
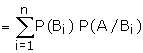
Proof:

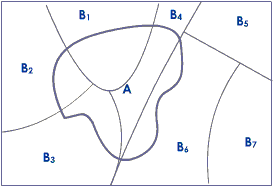
From the venn diagram, we have

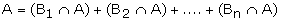
where 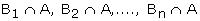are mutually exclusive events.

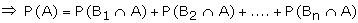
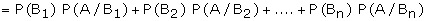
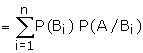
Baye's Theorem Let S be a sample space.

If A₁, A, A₃ ... A_n are mutually exclusive and exhaustive events such that P(A_i) ≠ 0 for all i.

Then for any event A which is a subset of

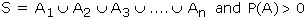
We have,

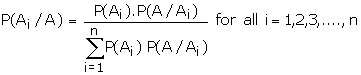
Proof:

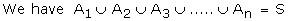
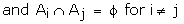
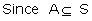
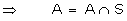
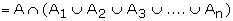
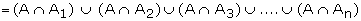
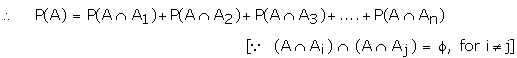
P(A) 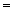P(A₁) P(A/A₁) +P(A₂)P(A/A₂)+�.+P(A_n) P(A/A_n) �.(1)

Also,

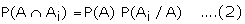
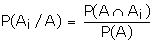
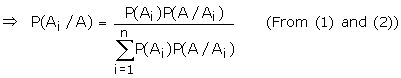
Example:

In a bolt factory 25%, 35% and 40% of the total is manufactured by machines A, B and C, out of which 5%, 4% and 2% are respectively defective. If the bolt drawn is found to be defective, what is the probability it is manufactured by the machine A?

Suggested answer:

Given P (A) = 0.25, P (B) = 0.35 and P (C) = 0.4 Let D be the event of getting a defective bolt.

P (D/A) = 0.05 P (D/B) = 0.04 P (D/C) = 0.02
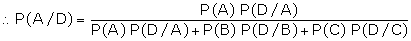
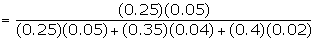
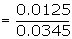
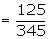