Binomial Distribution
A trial, which has only two outcomes
i.e., "a success" or "a failure", is called a Bernoulli trial.
Let X be the number of successes in a
Bernoulli trial, then X can take 0 or 1 and
P(X =1) = p = "probability of a
success"
P(X = 0) = 1 - p = q = "probability
of failure".
Consider a random experiment of
performing n independent Bernoulli trials.
Let p be the probability of success,
q = 1 - p be the probability of failure.
The probability of x successes and
consequently (n - x) failures in n independent trials in a specified
order say SSSFFSSFF�.FSF is given by
P(SSSFFSSFF�FSF)
= P(S) P(S) P(S) P(F) P(F) P(S) P(S)
P(F)�.P(F) P(S) P(F) = p.p.p.qq.ppq�.qpq
= pxqn-x
But x successes can occur in nCx
ways.
\ P(X = x)
= nCx px qn-x is the
probability mass function of exactly x successes.
The probability distribution of the
number of successes, so obtained is called the binomial distribution.
X P[X = x]
0 qn
1 nC1 pqn-1
2 nC2 p2
qn-2
3 nC3 p3
qn-3
n pn
Note 1:
n and p are called the parameters of
the binomial distribution.
Note 2:
If x is a binomial variate with
parameters n and p then it is denoted by x = b(n, p).
Note 3:
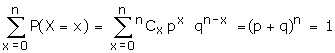
Example:
5 cards are drawn successively with
replacement from well shuffled deck of 52 cards. What is the probability
that
i) all the five cards are spades
ii) only 3 cards are spades
iii) none is a spade.
Suggested answer:
Let X be the random variable for the
number of spade cards drawn.
p = probability of drawing a spade
card
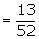
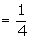
q = 1 - p
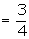
n = 5
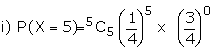
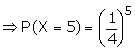
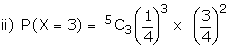
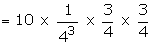
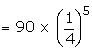
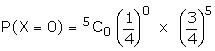
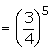
Recurrence Relation for the
Binomial Distribution We have
P(X = x + 1) = nCx+1
px+1 qn-x-1
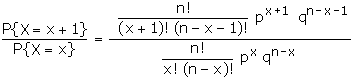
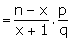
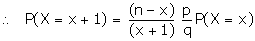 Mean and variance Mean and variance
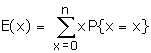
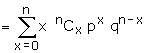
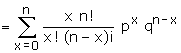
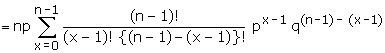
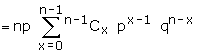
= np (p+q)n-1

To find the variance:
We have
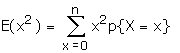
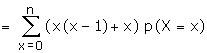
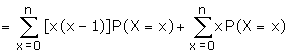
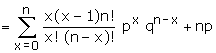
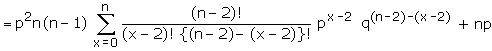
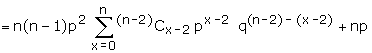
= n(n-1) p2 (p+q)n-2
+ np
= n2p2 - np2
+ np
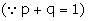
= n2p2 +
np(1-p)
= n2p2+ npq
Now V(x) = E(x2) - [E(x)]2
= n2p2 + npq -
n2 p2
= npq
Example:
If the mean and variance of a binomial distribution are respectively 9 and 6, find the distribution.
Suggested answer:
Mean of a binomial distribution = np
= 9
Variance of a binomial distribution =
npq = 6
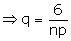
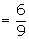
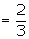

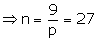
Binomial distribution is given by
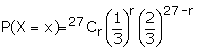
|