Conditional Probability
Let us consider the random experiment
of throwing a die. Let A be the event of getting an odd number on the
die.
\ S = {1,
2, 3, 4, 5, 6} and A = {1, 3, 5}
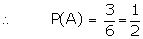
Let B = {2, 3, 4, 5, 6}. If, after
the die is thrown, we are given the information, that the event B has
occurred, then the probability of event A will no more be 1/2, because
in this case, the favourable cases are two and the total number of
possible outcomes will be five and not six.
The probability of event A,
with the condition that event B has happened will 2/5. This conditional
probability is denoted as P(A/B). Let us define the concept of
conditional probability in a formal manner.
Let A and B be any two events
associated with a random experiment. The probability of occurrence of
event A when the event B has already occurred is called the conditional
probability of A when B is given and is denoted as P(A/B). The
conditional probability P(A/B) is meaningful
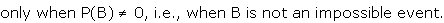
P(A/B) = Probability of occurrence of
event A when the event B as already occurred.

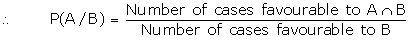

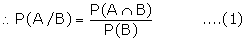
Remark 1:
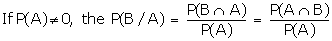
Remark 2:
If A and B are mutually exclusive
events, then
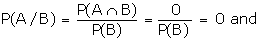
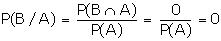
\ If A and
B are mutually exclusive events, then A/B and B/A are impossible events.
For an illustration, let us consider
the random experiment of throwing two coins.
\ S = {HH,
HT, TH, TT}
Let A = {HH, HT}, B = {HH, TH} and C
= {HH, HT, TH}
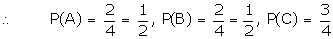
A/B is the event of getting A with
the condition that B has occurred.
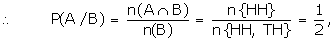
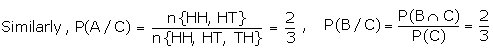
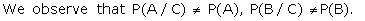
Remark 3:
We know that for the events A and B,
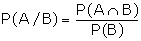
If B = S then
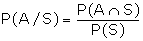
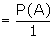
= P (A)
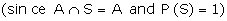
Remark 4:
If A = B
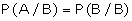
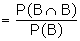
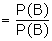
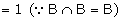
Remark 5:
From the formula of conditional
probabilities, we have
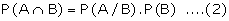
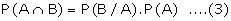
Equation (2) and equation (3) are
known as multiplication rules of probability for any two events A and B
of the same sample space.
Remark 6:
We know that two events are
independent if the occurrence of one does not effect the occurrence of
other. If A and B are independent events
P (A/B) = P (A) and P (B/A) = P (B)
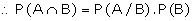
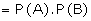
\ The
multiplication rule for the independent events A and B is given by
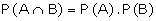
Remark 7:
So far, we have assumed that the elementary events are equally likely and we have used the corresponding
definition of probability. However the same definition of conditional
probability can also be used when the elementary events are not equally
likely. This will be clear from the following example.
Suppose a die is tossed. Let B be the
event of getting a perfect square.
The die is so constructed that the
event numbers are twice as likely to occur as the odd numbers.
Let us find the probability of B
given A, where A is the event getting a number greater than 3 while
tossing the die.
S = {1, 2, 3, 4, 5, 6}
If probability of getting an odd
number is x, the probability of getting an even number is 2x.
Since P (S) = 1
x + 2x + x + 2x + x + 2x = 1
9x = 1
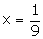
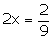


A = {4, 5, 6}
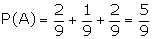
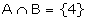
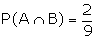
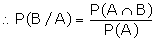
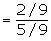
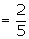
Example 1:
A card is drawn from an ordinary deck
and we are told that it is red, what is the probability that the card is
greater than 2 but less than 9.
Suggested answer:
Let A be the event of getting a card
greater than 2 but less than 9.
B be the event of getting a red card.
We have to find the probability of A given that B has occurred. That is,
we have to find P (A/B).
In a deck of cards, there are 26 red
cards and 26 black cards.
\ n(B) = 26
Among the red cards, the number of
outcomes which are favourable

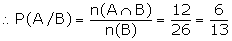
Example 2:
A pair of dice is thrown. If it is
known that one die shows a 4, what is the probability that
a) the other die shows a 5
b) the total of both the die is
greater than 7
Suggested answer:
Let A be the event that one die shows
up 4. Then the outcomes which are favourable to A are
(4, 1), (4, 2), (4, 3), (4, 4), (4,
5), (4, 6) (1, 4), (2, 4), (3, 4),
(5, 4), (6, 4)
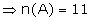
(a) Let B be the event of getting a 5
in one of the dies. Then the outcomes which are favourable to both A and
B are (4, 5), (5, 4)
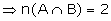
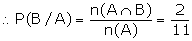
(b) Let C be the event of getting a
total of both the die greater than 7.
The out-comes which are favourable to
both C and A.
(4, 4), (4, 5), (4, 6), (5, 4), (6,
4)
\ n (C) =
5
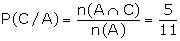
Note that in the above example P (B)
and P (B/A) are different.

Similarly P (C) and P (C/A) are
different.
|

