Events
 An event is the outcome or a combination of outcomes of an experiment. In other
words, an event is a subset of the sample space. e.g.,
{a head} in the experiment of tossing a coin is an event.
{a sum equal to 6} in the experiment of throwing a pair of dice is an
event. Occurence of an event Suppose we throw a die. Let E be the event of a
perfect square number. Then E = {1,4}. Suppose 3 appeared on the upper most
face, then we say that the event E has not occurred. E occurs only when 1 or 4
appears on the upper most face. Therefore whenever an outcome satisfies the
conditions, given in the event, we say that the event has occurred. In a
random experiment, if E is the event of a sample space S and w is the outcome,
then we say the event E has occurred if w
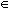E.
Types of Events S= {1,2,3,4,5,6}] If the event is set of elements
less than 2, then E = {1} is a simple event 1)
Simple Event: If an
event has one element of the sample space then it is called a simple or
elementary event.
Example: Consider the experiment of throwing a die.
Compound Event: If an event has more than one sample points, the
event is called a compound event . In the above example, of throwing a die,
{1, 4} is a compound event.
Null Event (f):
As null set is a subset of S, it is also an event called the null event or
impossible event. 4) The sample space S= {1, 2, 3, 4, 5, 6} in the above
experiment is a subset of S. The event represented by S occurs whenever the
experiment is performed. Therefore, the event represented by S is called a
sure event or certain event.
Complement of an Event: The
complement of an event E with respect to S is the set of all the elements of S
which are not in E.
The complement of E is denoted by E' or EC.
Note: In an experiment if E has not occurred then E' has occurred.
Algebra of Events In a random experiment, considering S(the sample space) as
the universal set, let A, B and C be the events of S. We can define union,
intersection and complement of events and their properties on S, which is
similar to those in set theory.
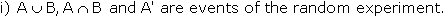
ii) A-B is an event, which is same as ''A but not B"
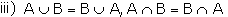
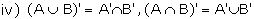
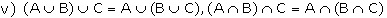
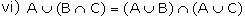
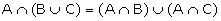
Example: Consider the same experiment throwing a die, then S= {1,
2, 3, 4, 5} Let A = {1, 2, 3, 4}, B = {2, 3, 4, 5} The following are also
events
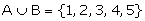
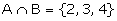A - B = {1} A'= {5, 6} Mutually Exclusive Events Two events
associated with a random experiment are said to be mutually exclusive, if both
cannot occur together in the same trial. In the experiment of throwing a die,
the events A = {1, 4} and B = {2, 5, 6} are mutually exclusive events. In the
same experiment, the events A = {1, 4} and C = {2, 4, 5, 6} are not mutually
exclusive because, if 4 appears on the die, then it is favourable to both events
A and C.
The definition of mutually exclusive events can also be extended to
more than two events. We say that more than two events are mutually exclusive,
if the happening of one of these, rules out the happening of all other events.
The events A = {1, 2}, B = {3} and C={6}, are mutually exclusive in connection
with the experiment of throwing a single die. If A and B are two events, then
A or B or (A
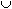B) denotes the event of the occurrence of at least one of the events A or B. A
and B or (A
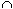B) is the event of the occurrence of both events A and B. If A and B happen to
be mutually exclusive events, then P(A
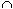B) = 0. For example, in the experiment of tossing three coins, if A and B be
the events of getting at least one head and at most one tail respectively, then
S = {HHH, HHT, HTH, THH, HTT, THT, TTH, TTT} A = {HHH, HHT, HTH, THH, HTT,
THT, TTH} B = {HHH, HHT, HTH, THH}
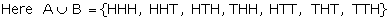
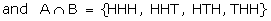E1, E2, �, En are n events associated with a
random experiment are said to be pairwise mutually exclusive,
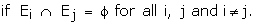For example, let a pair of dice be thrown and let A, B, C be the events "the
sum is 7", sum is 8, sum is greater than 10, respectively.
\ A = {(1, 6), (2, 5), (3, 4), (4, 3), (5, 2), (6, 1)} B = {(2,6),
(3,5), (4,4), (5,3), (6,2)} and C = {(5,6), (6,5), (6,6)} The events A, B and
C are pairwise mutually exclusive. Two events A and B are said to be mutually
exclusive if the occurrence of A prevents the occurrence of B and vice versa.
Exhaustive Events For a random experiment, let E1, E2, E3,�..
En be the subsets of the sample space S. E1, E2,
E3, � En form a set of Exhaustive events if
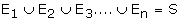A set of events E1, E2, E3, �. En
of S are said to mutually exclusive and exhaustive events if
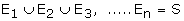
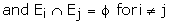
Example:
In tossing of a coin, there are two exhaustive cases, {H}, {T}.
In throwing of a dice, there are 6 exhaustive cases, {1}, {2}, {3}, {4}, {5},
{6}.
In throwing of a pair of dice, there are 36 exhaustive cases. Example of an
event which is exhaustive, but not mutually exclusive. In throwing a die
experiment, let E1 represent the outcomes which are less than 4, E1=
{1,2,3}.
Let E2 represent the outcomes which are greater than 2, E2=
{3,4,5,6}.
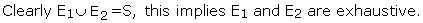
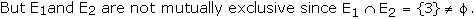
Let E3 represent the outcomes which are greater than 4, E3
={5, 6}. Clearly E1 and E3 are mutually exclusive, but
not exhaustive. Let E4 ={2, 4, 6} and E5 = {1, 2, 5}
Then E4 and E5 are mutually exclusive and exhaustive
since.
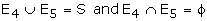
Equally Likely Outcomes The outcomes of a random experiment are said to be
equally likely, if each one of them has equal chance of occurrence. Example:
The outcomes of an unbiased coin are equally likely.
|
