Multiplication Rule of Probability
We have already proved that if two
events A and B from a sample S of a random experiment are mutually
exclusive, then
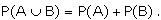
In this section, we examine whether
such a rule exists, if '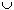 '
is replaced by ' '
is replaced by '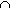 '
and '+' is replaced by 'x' in the above addition rule. If it does exist,
what are the particular conditions restricted on the events A and B. '
and '+' is replaced by 'x' in the above addition rule. If it does exist,
what are the particular conditions restricted on the events A and B.
This leads us to understand the
dependency and independency of the events.
Example:
A bag contains 5 white and 8 black
balls, 2 balls are drawn at random. Find
a) The probability of getting both
the balls white, when the first ball drawn, is replaced.
b) The probability of getting both
the balls white, when the first ball is not replaced.
Suggested answer:
a) The probability of drawing a white
ball in the first draw is 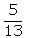 .
Since the ball is replaced, the probability of getting white ball in the
second draw is also .
Since the ball is replaced, the probability of getting white ball in the
second draw is also
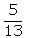 . .

b) The probability of drawing a white
ball in the first draw is
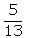 .
If the first ball drawn is white and if it is not replaced in the bag,
then there are 4 white balls and 8 black balls. Therefore, the
probability of drawing a white ball in the second draw = .
If the first ball drawn is white and if it is not replaced in the bag,
then there are 4 white balls and 8 black balls. Therefore, the
probability of drawing a white ball in the second draw =
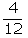 . .
In this case, the probability of
drawing a white ball in the 2nd draw depends on the
occurrence and non-occurrence of the event in the first draw.
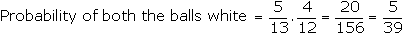 Independent Events
Independent Events
Events are said to be independent if
the occurrence of one event does not affect the occurrence of others.
Observe in case(a) of above example,
The probability of getting a white
ball in the second draw does not depend on the occurrence of the event
on the first draw.
However in case(b), the probability
of getting a white ball in the second draw depends on the occurrence and
non - occurrence of the event in the first draw.
It can be verified by different
example.
If A and B are two independent
events, then
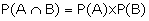
This is known as Multiplication
Rule of Probability.
The converse is also true, that is if
two events A and B associated with a random experiment are such that
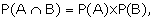
then the two events are independent.
Two events are said to be dependent
if the occurrence of one affects the occurrence of the other. In this
case,
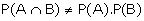
In the above example,
let
A = event that the outcome is a white
ball in the first draw
B = event that the out come is a
white ball in the second draw
In case (a),
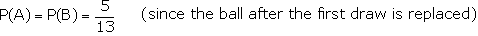
\ The
probability that both the balls drawn is white
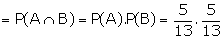
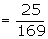
In case (b),
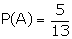
(Since the ball after the first draw is not replaced)
P(B) = P (first draw is white and second draw is white)
+ P (first draw is black and second draw is white)
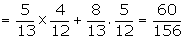
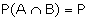 (both the balls are white)
(both the balls are white)
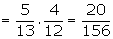
Here P(A
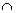 B) B)
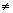 P (A). P(B) since the events are not independent. Independent Experiment
P (A). P(B) since the events are not independent. Independent Experiment
Two random experiments are said to be
independent if for every pair of events E and F, where E is associated
with the first experiment and F is associated with the second
experiment, the probability of simultaneous occurrence of E and F, when
the two experiments are performed, is the product of the probabilities
P(E) and P(F), calculated separately on the basis of the two
experiments.
i.e,. P(E F)=
P(E).P(F) F)=
P(E).P(F)
Example:
Probability of solving a specific problem independently by A and B are 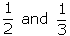 respectively. If both try to solve the problem independently, find the
probability that the problems be solved.
respectively. If both try to solve the problem independently, find the
probability that the problems be solved.
Suggested answer:
Let A be the event of A solving the problem.
Let B be the event of B solving the problem.
Then,
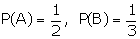
P (A not solving the problem)
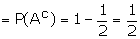
P (B not solving the problem)
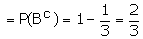
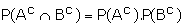
(Considering the experiments as independent, because A and B solve the problem independently)
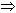 P (both not solving the problem) P (both not solving the problem)
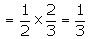
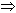 Probability that the problem can be solved Probability that the problem can be solved
Note:
If A and B are independent, then
i) Ac and Bc
are independent
ii) Ac and B are
independent
iii) A and Bc are
independent
|

