Poisson Distribution

Poisson distribution is a limiting process of binomial distribution. Poisson
distribution occurs when there are events which do not occur as outcomes of a
definite number of outcomes.
Poisson distribution is used under the following conditions:
 Number of trials n tends to infinity
Number of trials n tends to infinity
 Probability of success p tends to zero and
Probability of success p tends to zero and
 np = l is finite.
np = l is finite.
Poisson Distribution as a Limiting Form of the Binomial Distribution We shall
now deduce the Poisson distribution from the binomial distribution by assuming
that n � � and p � 0 such
that the product np always remains finite, say l.

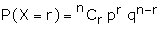
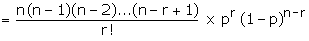
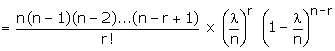
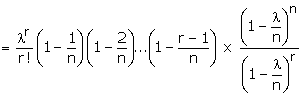
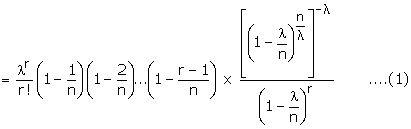
We shall now use a very important result of limits in Calculus. We state this
result without proof:
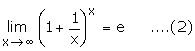
where e is a constant lying between the number 2 and 3 and ex is
defined by
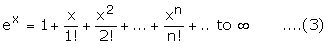
with x a real number. From equation (1), we observe that each of (r - 1)
factors,
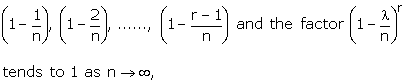
 that
that
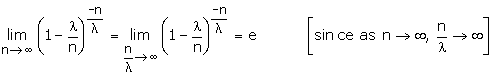
Thus
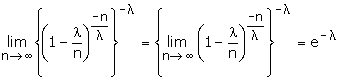
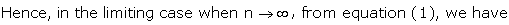
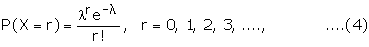
where l is a finite number and is equal to np.
The sum of the probabilities P(X = r) or simply P(r) for r = 0, 1, 2, � is 1.
This can be seen by putting r = 0, 1, 2, � in (4) and adding all the
probabilities.
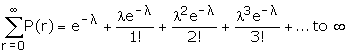
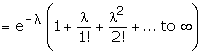
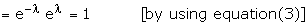
Also, each of the probabilities is a non-negative fraction. This leads to the
distribution defined below:
A random variable X taking values 0, 1, 2, � is said to have a Poisson
distribution with parameter l (finite), if its
probability distribution is given by
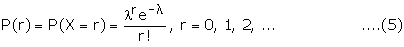
There are many daily life situations where n is very large and p is very
small. In such situations, the Poisson distribution can be more conveniently
used as an approximation to binomial distriburtion which may prove cumbersome
for large values of n. This is called Poisson approximation to binomial
distribution. The Poisson approximation to binomial distribution is easier to
compute directly and easier to tabulate than the binomial distribution, since
the values of e-l for various
values of l are found in standard tables. Some
examples of such situations are i) telephone trunk lines with a large number
of subscribers and the probability of telephone lines being available is very
small, ii) traffic problems with repeated occurrence of events such as
accidents whose probability is very small, iii) many industrial processes
undergoing mass scale production with probability of events as 'faults' or
'breakdowns' being very small, etc. The probability mass function of the
Poisson distribution given by
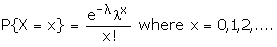
Note 1:
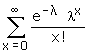
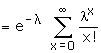
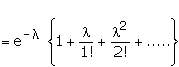 = e-l el
= 1
= e-l el
= 1
Example: A random variable X has a Poisson distribution with
parameter l such that P (X = 1) = (0.2) P (X = 2).
Find P (X = 0).
Suggested answer: For the Poisson distribution, the probability
function is given by

Given P (x = 1) = (0.2) P (X = 2)
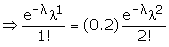
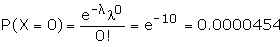
Recurrence Relation for the Probabilities of Poisson Distribution
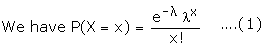
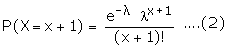

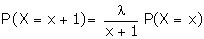
Mean and Variance
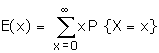
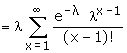
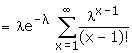
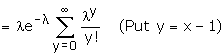 = le-l
el = l
= le-l
el = l
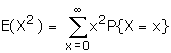
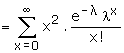
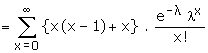
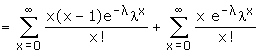
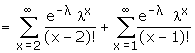
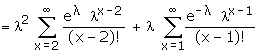
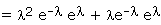
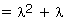
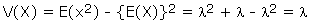
Example: If the variance of the Poisson distribution is 2, find the
probabilities for r = 1, 2, 3, 4 and 5 from the recurrence relation of the
Poisson distribution.
Suggested answer:
The variance of the Poisson distribution
= l = 2
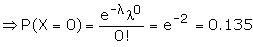
Recurrence relation is given by
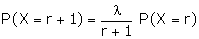
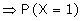
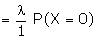
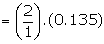
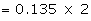
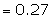
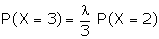
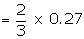
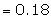
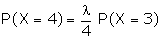
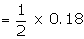
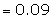
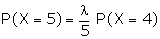
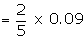
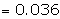
|