Probability of an Event

Probability of an Event

So far, we have introduced the sample of an experiment and used it to describe events. In this section, we introduce probabilities associated to the events. If a trial results in n-exhaustive, mutually exclusive and equally likely cases and m of them are favourable to the occurrence of an event A, then the probability of the happening of A, denoted by P(A), is given by

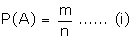
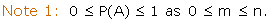
Note 2:

If P(A) = 0 then A is called a null event, or impossible event.

Note 3:

If P(A) = 1 then A is called a sure event.

Note 4:

If m is the number of cases favourable to A. Then m - n is favourable to "non occurrence of A

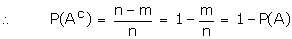
Note 5: If the odds are a:b in favour of A then

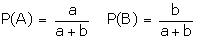
This is the same as odds are b:a against the event A. Statistical or Empirical Probability If a trial is repeated N number of times under essential homogeneous


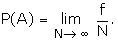
Axiomatic Approach to Probability Axiomatic approach to probability closely relates the theory of probability to set theory. Let S be the sample space of an experiment. Probability is a function, which associates a non-negative real number to every event A of the sample space denoted by P(A) satisfying the following axioms. For every event A in S, P(A) � 0. P(S) = 1. If A₁, A₂, A₃,�.A_n are mutually exclusive events in S, then
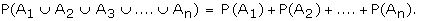