Random Variable and Probability Distribution
If is often very important to allocate a numerical value to an outcome of a
random experiment. For example consider an experiment of tossing a coin twice
and note the number of heads (x) obtained. Outcome : HH HT TH TT No. of
heads (x) : 2 1 1 0 x is called a random variable, which can assume the values
0, 1 and 2. Thus random variable is a function that associates a real number to
each element in the sample space.
Random variable (r.v) Let S be a
sample space associated with a given random experiment. A real valued function
X which assigns to each wi �
S, a unique real number.
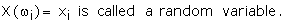
Note: There can be several r.v's associated with an experiment. A
random variable which can assume only a finite number of values or countably
infinite values is called a discrete random variable. e.g., Consider a random
experiment of tossing three coins simultaneously. Let X denote the number of
heads then X is a random variable which can take values 0, 1, 2, 3.
Continuous random variable A random variable which can assume all possible
values between certain limits is called a continuous random variable.
Discrete Probability Distribution A discrete random variable assumes each
of its values with a certain probability, Let X be a discrete random variable
which takes values x1, x2, x3,�xn
where pi = P{X = xi} Then X : x1 x2
x3 .. xn P(X): p1 p2 p3
..... pn is called the probability distribution of x.
Note 1:
In the probability distribution of x
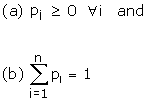
Note 2: P{X = x} is called probability mass function.
Note 3:
Although the probability distribution of a continuous random variable cannot
be presented in tabular form, it can have a formula in the form of a function
represented by f(x) usually called the probability density function.
Probability distribution of a continuous random variable Let X be
continuous random variable which can assume values in the interval [a,b]. A
function f(x) on [a,b] is called the probability density function if
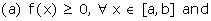
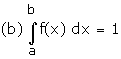Mean and Variance of a Discrete Random Variable Let X be a discrete random
variable which can assume values x1, x2, x3,�xn
with probabilities p1, p2, p3 �.. pn
respectively then (a) Mean of X or expectation of X denoted by E(X) or
m is given by
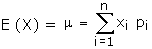
(b) Variance of X denoted by s2 is given
by
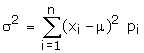
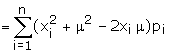
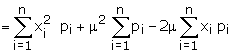
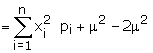
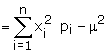
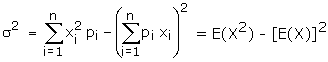
Note :
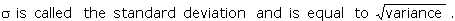
Example : Two cards are drawn successively without replacement, from a
well shuffled deck of cards. Find the mean and standard deviation of the random
variable X, where X is the number of aces.
Suggested answer: X is the
number of aces drawn while drawing two cards from a pack of cards. The total
ways of drawing two cards 52C2. Out of 52 cards these are
4 aces. The numbers of ways of not drawing an Ace =48C2.
The number of ways of drawing an ace is 4C1 x 48C1
and two aces 4C2. Therefore the r.v. X can take the
values 0, 1, 2.
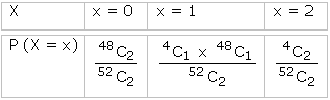
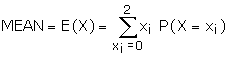
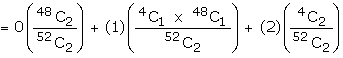
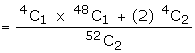
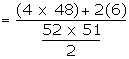
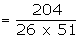
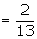
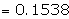
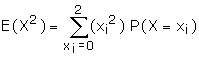
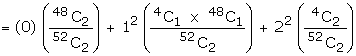
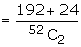
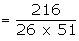
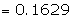
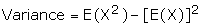= 0.1629 - 0.0236 = 0.13925
Let X be a continuous random variable which can assume values in (a, b) and
f(x) be the probability density of x then (a) Mean of X or Expectation of X is
given by
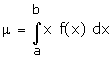(b) Variance of x is given by
|
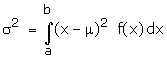
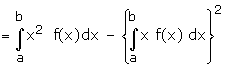
