Random Variables and Probability Distributions
It is often very important to allocate a numerical value to an outcome of a
random experiment. For example, consider an experiment of tossing a coin twice
and note the number of heads (x) obtained. Outcome HH HT TH TT No. of
heads (x) 2 1 1 0 x is called a random variable, which can assume the values
0, 1 and 2.
Thus, random variable is a function that associates a real number to
each element in the sample space. Random variable (r.v) Let S be a sample
space associated with a given random experiment.
A real valued function X which assigns to each wi
� S, a unique real number, X(wi)
= xi is called a random variable.
Note: There can be several r.v's associated with an experiment. A
random variable which can assume only a finite number of values or countably
infinite values is called a discrete random variable. e.g., Consider a random
experiment of tossing three coins simultaneously. Let X denote the number of
heads obtained. Then, X is a r.v which can take values 0, 1, 2, 3. Continuous
random variable A random variable which can assume all possible values between
certain limits is called a continuous random variable. Discrete probability
distribution A discrete random variable assumes each of its values with a
certain probability.
Let X be a discrete random variable which takes values x1,
x2, x3,�xn where pi = P{X = xi}
Then X : x1 x2 x3 �xn P(X) : p1
p2 p3 � pn is called the probability
distribution of x, If in the probability distribution of x,
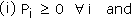
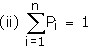
Note 1 : P{X = x} is called probability mass function.
Note 2:
Although the probability distribution of a continuous r.v cannot be presented
in tabular forms, we can have a formula in the form of a function represented by
f(x) usually called the probability density function.
|