Theorems of Probability
Theorem 1:(Addition Rule of Probability)
If A and B are any two events,
then
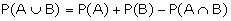Proof:
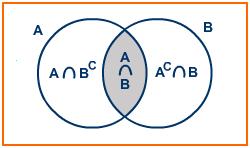
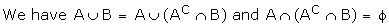(From the Venn diagram)
(
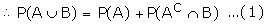
A and AC
B are mutually exclusive)
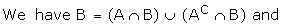
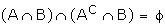
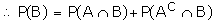
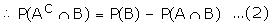
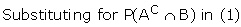
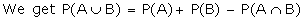
Note 1:
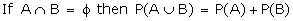
If A and B are mutually exclusive events, then P(A
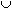B) = P(A) + P(B)
Note 2: If A, B, C are any three events, then
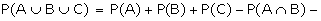
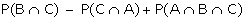
Example: In tossing a fair die, what is the probability that the
outcome is odd or grater than 4? Suggested answer: Let E1
be the event that the outcomes are odd. E1 = {1,3,5} Let E2
be the event that the outcomes are greater than 4. E2 = {5,6}
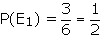
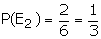
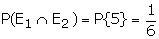
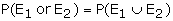
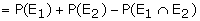
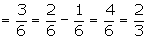
Theorem 2:
P(AC) = 1 - P(A) Proof:
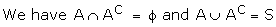
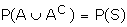
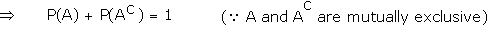\ P(A) = 1 - P(AC)
Example:
In tossing a die experiment, what is the probability of getting at least 2.
Suggested answer: Let E be the event that the outcome is at least 2, then
E = {2,3,4,5,6} EC= {1}
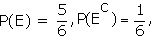
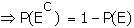
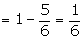
Theorem 3: P(f) = 0 Proof: The proof
follows from theorem 2, P(f)C = 1 - P(f)
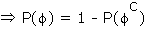
= 1 - 1 = 0
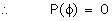
Example:
In throwing a die experiment, what is the probability of
occuring a number greater than 8 ? Suggested answer: Let E be the
event where the outcome is greater than 8. E = f
P(f) = 0
|
